[UCPC][2019][예선] H번 풀이

풀이

삼성 SW 엑스퍼트 사이트의 개인 역량 확인 문제가 생각나는 문제입니다. 물론 그것보다는 많이 어려웠습니다.

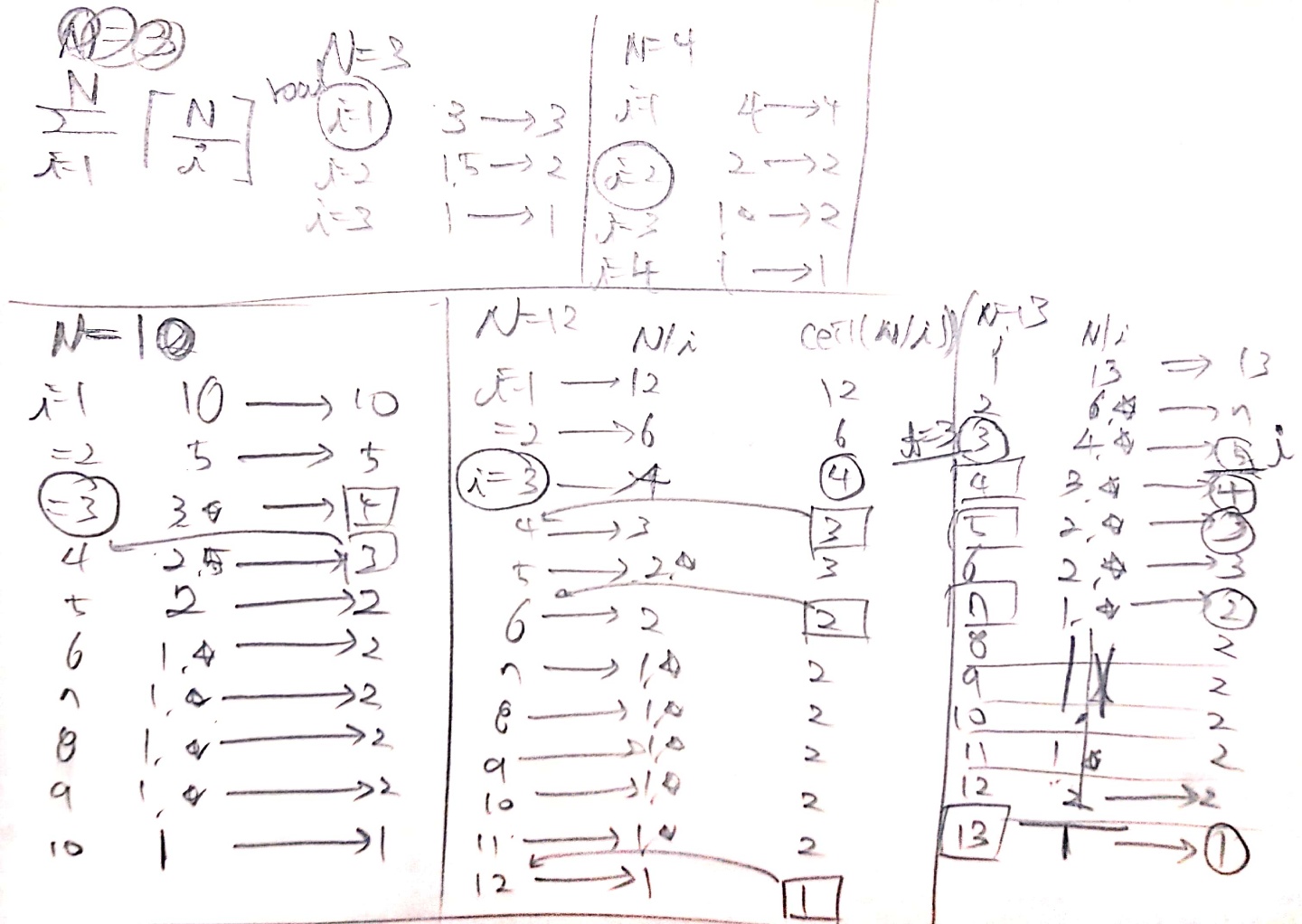
6번째 줄이 어떤 의미인지 이해하는 것은 이 문제에서 중요하지 않습니다. 4번째 줄은 i가 1부터 n까지 1씩 증가하므로 n번 실행됩니다. 5번째 줄은 j가 1부터 n까지 커지는데 커지는 양(이하 step)이 1,2,3, …,n-1, n으로 증가합니다.

따라서

[1,n]에서 step이 1일 때 몇 개를 지나는가? +
[1,n]에서 step이 2일 때 몇 개를 지나는가? +
…
[1,n]에서 step이 n-1일 때 몇 개를 지나는가? +
[1,n]에서 step이 n일 때 몇 개를 지나는가?

를 모두 더하면 됩니다.

[1,n]에서 step이 a일 때 몇 개를 지나는가?는 ceil(n/a)로 얻을 수 있습니다. 단, ceil()의 정의에 따라서 전달되는 값은 double 형태여야 원하는 출력값을 얻을 수 있습니다. (ceil()은 double 타입 값을 받아서 올림을 한 뒤 이를 만족하는 가장 작은 정수값을 int로 반환합니다.)

시간 초과 코드

가장 기본적으로 아래와 같은 코드를 생각할 수 있습니다.

#include <cstdio>
#include <cmath>
using namespace std;
typedef long long ll;
ll n; //read
ll ans = 0;//answer

int main(void) {
	scanf("%lld", &n);
	for (int i = 1; i <= n; i++) {
		ans += ll(ceil(n / double(i)));
	}
	printf("%lld\n", ans);
	return 0;
}

이렇게하면 모든 TC를 맞출 수는 있지만 n이 10의 9승까지 주어질 수 있으므로 시간 초과가 나옵니다.

시간초과 해결법 및 풀이

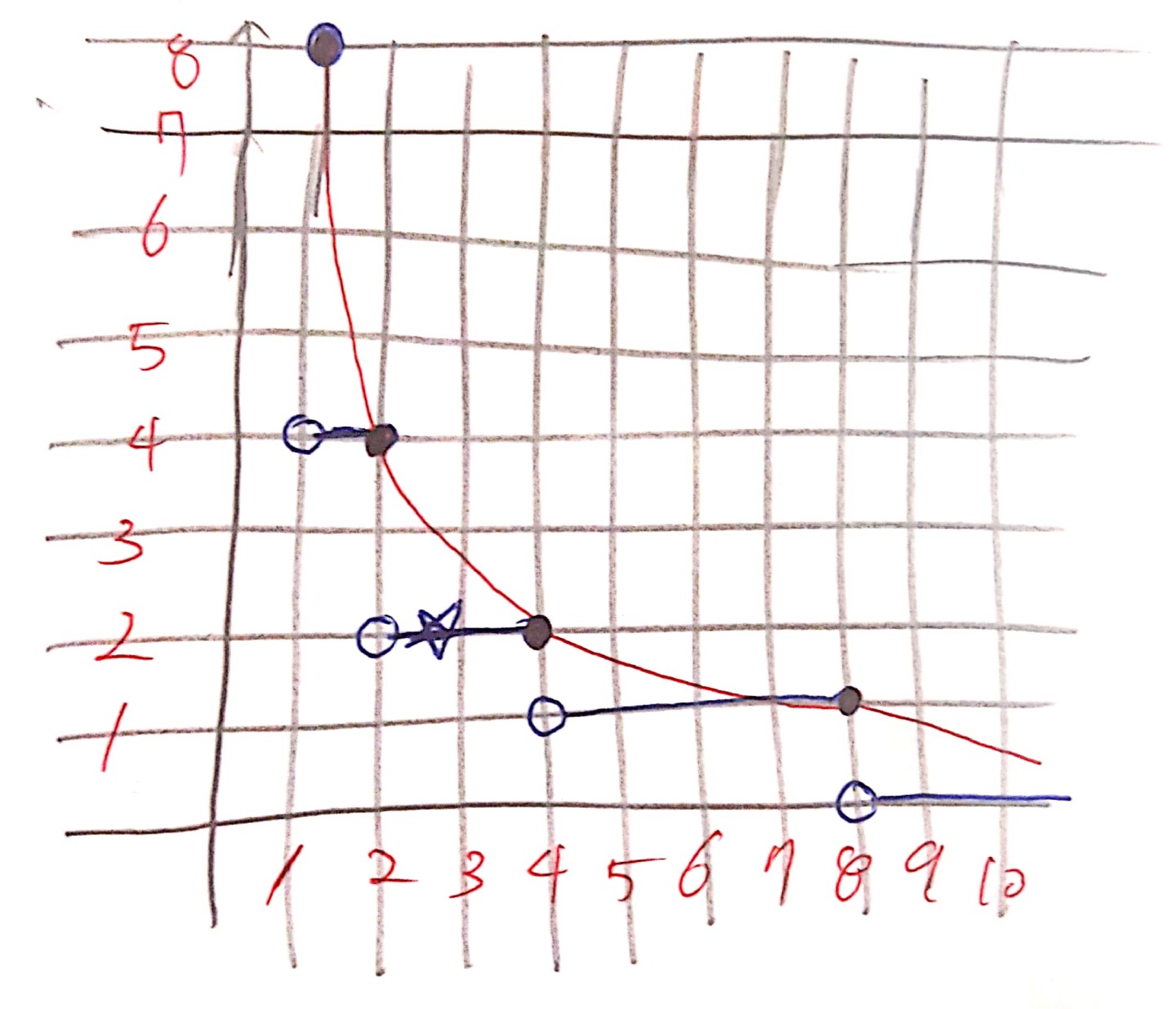
위 그림은 $y=8/x$ 그래프를 나타냅니다. 그리고 파란색으로 그린 부분은 $y=[8/x]$를 대략적으로 나타냅니다. 위 그림이 의미하는 바는, $y=[상수/x]$의 그래프에서 x값이 1증가할 떄마다 계속해서 결과값이 바뀌는 것이 아니라 같은 결과가 계속해서 나오는 구간이 있음을 나태냅니다. 따라서 $10^{9}$번 ceil()을 호출하지않고 전체의 합을 구할 수 있습니다.

$y=[n/x]$를 그려서 생각해보면 x가 $n^{1/2}$가 되는 시점부터는 y의 값이 이전 값과 같거나 1씩 작아지는 것을 알 수 있습니다. 왜 그런지 곰곰히 생각해봤는데, 그냥 저 그래프의 특성이라고 생각해야할 것 같습니다.

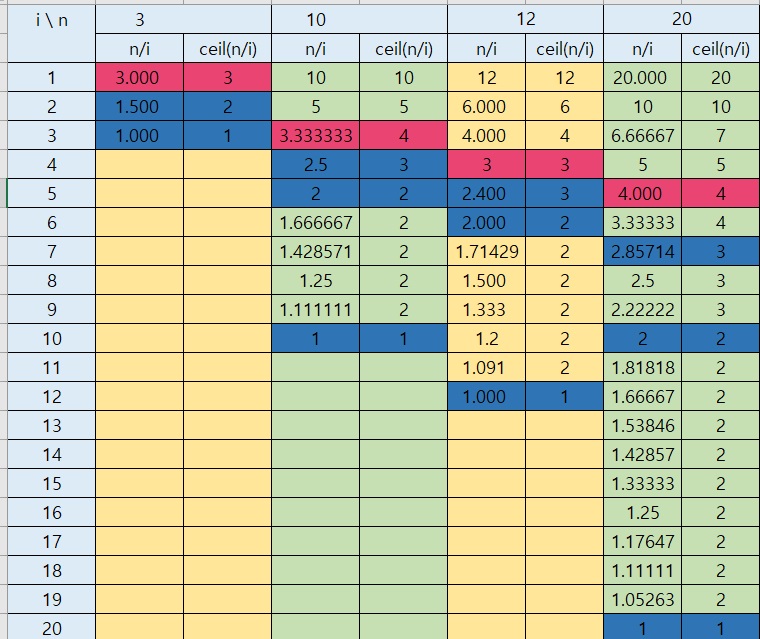
위 표는 n이 3,10, 12, 20일 때, 그리고 $1<=i<=n$일 때 n/i와 ceil(n/i)의 값을 나타냅니다. 빨간색으로 표시된 부분은 round(sqrt(n))의 값을 나타냅니다. 이 지점 이후부터는 ceil(n/i)의 값이 이전값과 같거나 1이 작은 값을 가집니다. 반면에 빨간셀 이전에는 들쑥날쑥한 값을 가집니다. 그리고 파란색으로 표시된 셀은 ceil(n/i)의 값이 언제 바뀌는지를 표시한 것입니다.

시간초과를 해결하는 핵심은 $10^{9}$q번의 ceil()을 호출하는 것이 아니라 아래와 같이 두 영역으로 구분해서 ceil()을 호출하는 횟수를 줄이는 것입니다.

1. i가 1부터 빨간색셀을 만나기 전까지는 i+=1 시키면서 ceil(n/i)를 호출하기
2. 빨간색셀부터는 파란색셀의 위치를 파악해서 같은 ceil(n/i)의 결과가 나오는 i에서는 ceil()를 호출하지 않기

참고로, $sqrt(10^{9})$의 값은 대략 31622.776602입니다. 따라서 가장 큰 n의 경우에도 1번 과정을 진행하는 것은 주어진 시간 내에 문제를 해결하는데 문제가 없습니다.

#include <iostream>
#include <cmath>
#include <vector>
using namespace std;
typedef long long ll;
ll n; //read
vector<ll> v;
ll ans = 0;//answer

int main(void) {
	scanf("%lld", &n);
	//루트 씌우고 내림해서 t 정의
	double t = floor(sqrt(n));
	v.push_back(t);
	//[1,t)까지는 일일이 다 계산해서 더하기
	for (double k = 1; k < t; k += (1.0)) {
		ans += ll(ceil(n / k));
	}
	//[t,n)까지 ceil의 값이 바뀌는 구간 저장하기
	double i = (ceil(n / t));
	for (i -= 1; i > 0; i--) {
		v.push_back(ll(ceil(n/i)));
	}
	/*//[t,n)까지 ceil의 값이 바뀌는 구간 확인하기
	for (int i = 0; i < v.size(); i++) {
		cout << v[i] << "\n";
	}*/
	//저장된 구간에 대해서 [v[i],v[i+1]) * ll(ceil(n/v[i])) 더하기
	for (double i = 0; i < v.size() - 1; i += 1.0) {
		ans += (v[i + 1] - 1 - v[i] + 1) * ll(ceil(n / double(v[i])));
	}
	ans += 1;
	cout << ans << "\n";
	return 0;
}