[1767][미완성] 프로세서 연결하기

DFS 풀이

1. 가장자리에 있지 않은 모든 코어를 queue에 넣는다.
2. dfs(idx)를 진행하는데, idx는 몇 번째의 core에 대해서 4방향으로 연결을 시도할 것인지를 나타낸다.
3. dfs(idx)의 종료 조건은 마지막 idx의 core까지 모두 연결을 시도한 순간이 된다.
4. idx번째의 core에 대해서 4방향으로 연결을 시도하고, 만약 연결이 가능하면 idx번째의 core는 해당 방향으로 연결된 것으로 간주하고 dfs(idx+1)한다.
5. 만약 4방향 모두로 연결이 불가능하다면 idx번째의 core는 연결이 불가능한 것이므로 dfs(idx+1)을 한다.

DFS 코드

//NOT-YET
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;

int map[12][12];
int dx[] = { 0,0,1,-1 };
int dy[] = { 1,-1,0,0 };
int n = 0;
pair<int, int> ans = { 0,0 };
//ans.first : 몇 개를 연결했는가?
//ans.second : ans.first개를 연결하기 위해서 몇 개의 전선을 사용했는가?
vector<pair<int, int> > core; //테두리에 있지 않은 코어들

void dfs(int idx, pair<int, int> tans) {
	if (idx == core.size()) {
		//모든 코어를 다 점검한 경우
		if (ans.first < tans.first) ans = tans;
		else if (ans.first == tans.first && ans.second > tans.second) ans = tans;
		return;
	}
	int impos = 0;
	for (int k = 0; k < 4; k++) {
		if (connect(core[idx].first, core[idx].second, k)) {
			tans.first += 1;
			dfs(idx + 1, tans);
		}
		else impos += 1;
		disconnect(core[idx].first, core[idx].second, k);
	}
	if (impos == 4) dfs(idx + 1, tans);
}

bool connect(int i, int j, int dir) {
	//dir 방향으로 전선을 깔아보기
	while (true) {
		i += dx[dir];
		j += dy[dir];
		if (map[i][j] == 0) map[i][j] = 1;
		else if(map[i][j] == 1) 
	}
	return true;
}
bool disconnect(int i, int j, int dir) {
	//dir 방향으로 전선을 지우기
	return true;
}

int main(void) {
	int tcase = 0; scanf("%d", &tcase);
	for (int tc = 1; tc <= tcase; tc++) {
		int ans = 0;
		memset(map, 0, sizeof(map));
		core.clear();
		scanf("%d", &n);
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				scanf("%d", &map[i][j]);
				if (i == 0 || i == n - 1) continue;
				if (j == 0 || j == n - 1) continue;
				if(map[i][j] == 1 ) core.push_back(make_pair(i, j));
			}
		}
		dfs(0,make_pair(0,0));
		printf("#%d %d\n", tc, ans);
	}
	return 0;
}

[시간초과 Brute-Force] 풀이

1. N의 최대값이 12이고, 코어의 최대 갯수가 12개이므로 $$Brute-Force임을 짐작할 수 있다.
2. 모든 경우의 수를 커버하는 방법은 다음과 같다. 각 시도마다 각각의 코어들이 연결될 방향이 결정되어 있다.
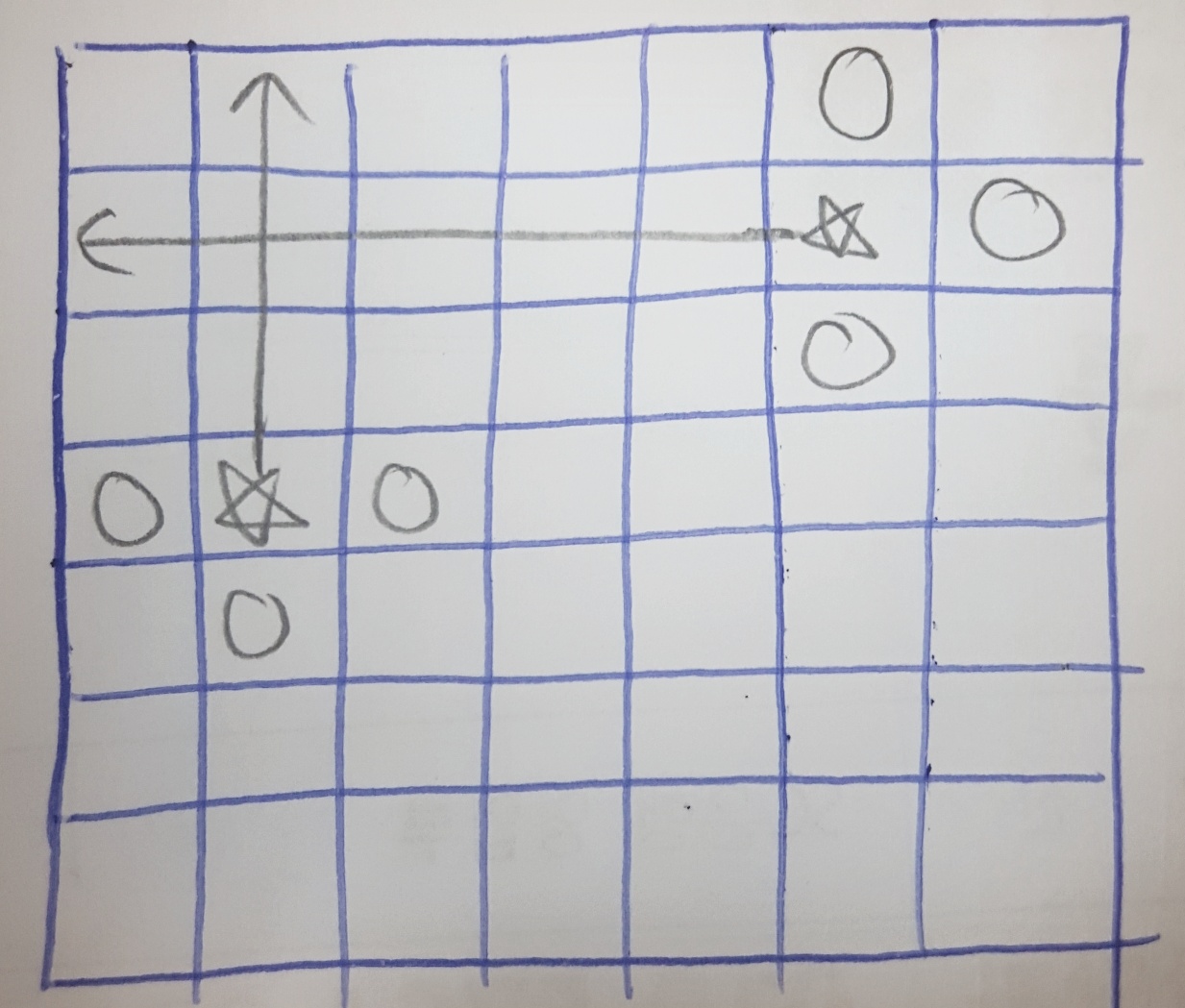
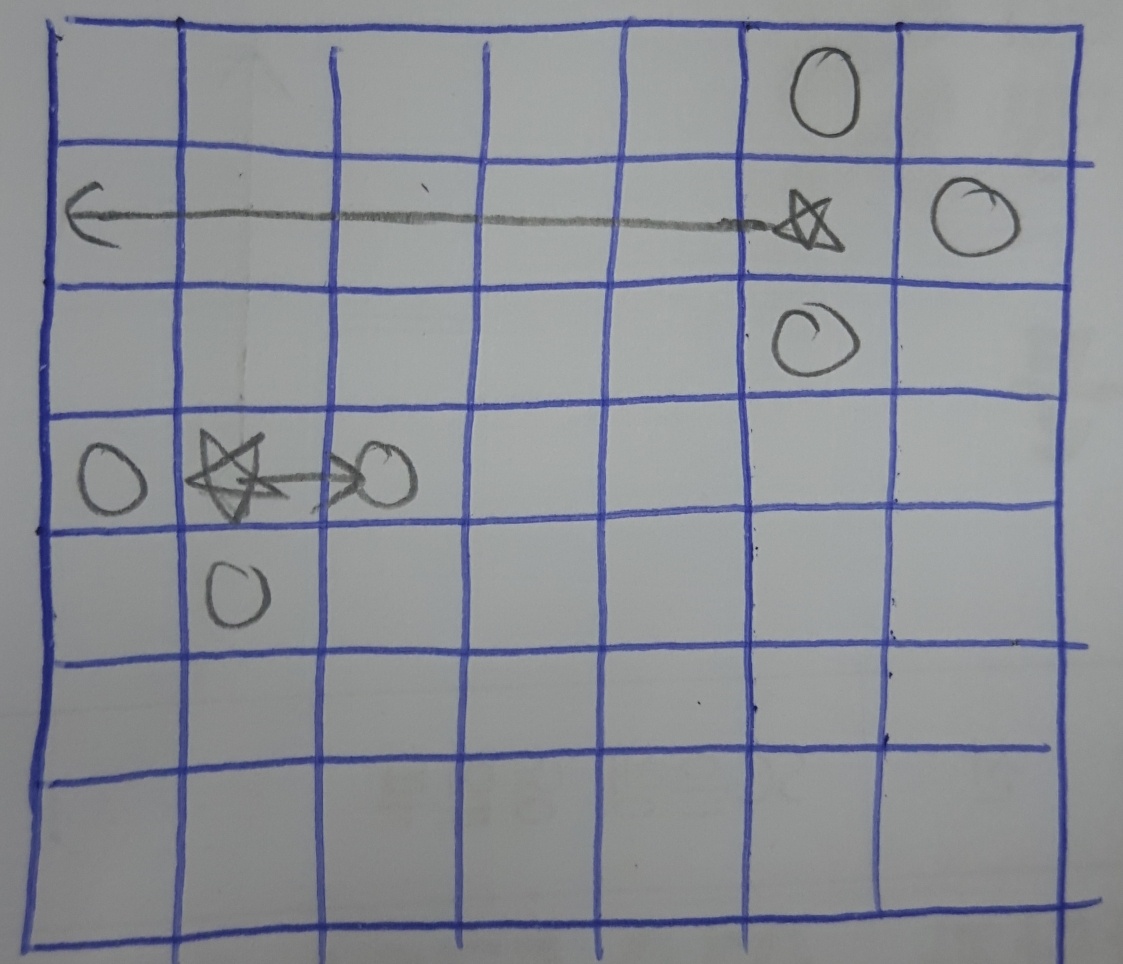
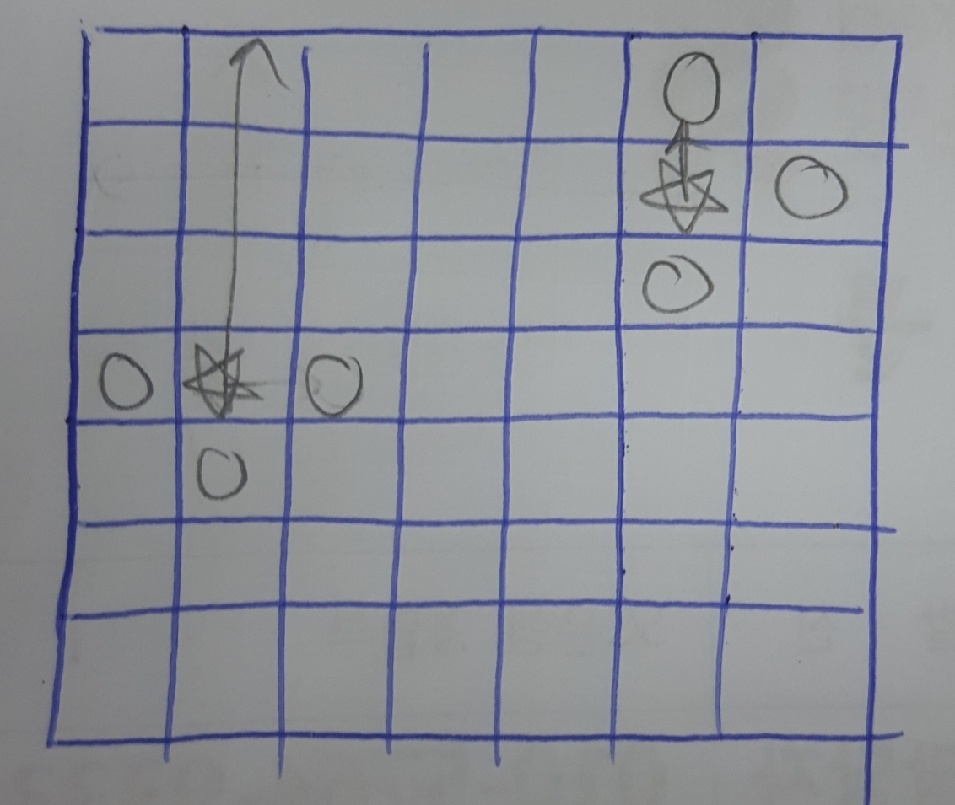
3. 코어 A를 할당된 방향으로 연결하고 코어 B에 할당된 방향으로 연결하면서 전선이 겹친다면 이 경우를 그냥 제외하면 된다. 왜냐하면 코어 A와 B에 할당된 방향이 각각 전원과 연결될 가능성이 있는 유일한 방향이라면, 둘 중 하나만 유일한 가능성의 방향으로 할당되고, 나머지 하나는 아예 가능성이 없는 방향으로 할당된 경우의 수도 고려하기 때문에 모든 수를 고려할 수 있다. 아래와 같이 첫 번 째 사진의 경우를 무시해도 되는 것은 두, 세 번째의 경우를 모두 고려하기 때문이다.

구글 코드

#include <cstdio>
#include <vector>
using namespace std;
 
int t,n,map[12][12],cnt,cnt2,dx[4]={0,0,1,-1},dy[4]={1,-1,0,0},CORE,SUM;
vector<pair<int,int>> core;
vector<int> v;
 
void solve()
{
    int tmap[12][12];
    for(int i=0;i<n;i++) for(int j=0;j<n;j++) tmap[i][j]=map[i][j];
    int sum=0,c=cnt2;
    for(int i=0;i<cnt;i++)
    {
        int x=core[i].first,y=core[i].second;
        while(true)
        {
            x+=dx[v[i]],y+=dy[v[i]];
            if(x<0 || x>=n || y<0 || y>=n) { c++; break; }
            if(tmap[x][y]==1) return;
            else tmap[x][y]=1,sum++;
        }
    }
    if(CORE<c) CORE=c,SUM=sum;
    else if(CORE==c && SUM>sum) SUM=sum;
}
 
void go(int n)
{
    if(n==cnt)
    {
        solve();
        return;
    }
    for(int i=0;i<4;i++)
    {
        v.push_back(i);
        go(n+1);
        v.pop_back();
    }
}
 
int main()
{
    scanf("%d",&t);
    for(int k=1;k<=t;k++)
    {
        scanf("%d",&n);
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<n;j++)
            {
                scanf("%d",&map[i][j]);
                if(map[i][j]==1)
                {
                    if(i==0 || i==n-1 || j==0 || j==n-1) cnt2++;
                    else core.push_back({i,j}),cnt++;
                }
            }
        }
        go(0);
        printf("#%d %d\n",k,SUM);
        core.clear(),cnt=cnt2=CORE=SUM=0;
    }
    return 0;
}