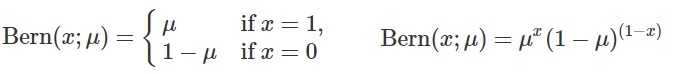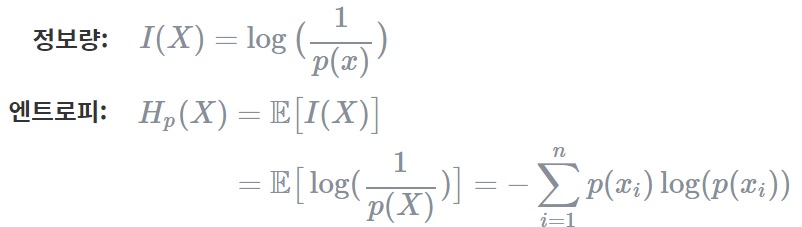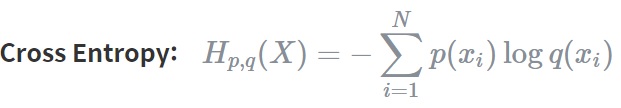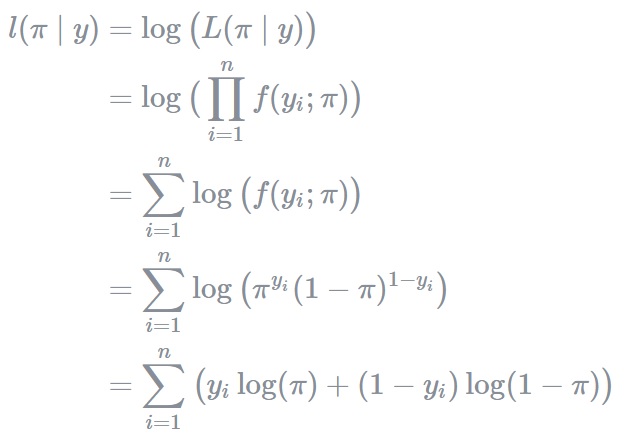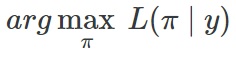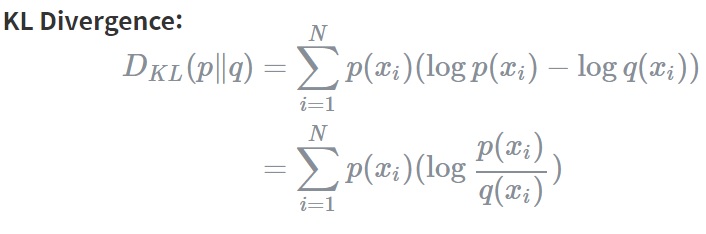[ML][GAN] Chapter 0
Goal : GAN(Generative Adversarial Networks)
개요
ML을 배울 때 처음 접하는 classification이나 image segmentation 모델은 대상을 판별(Discrimiate)라는 네트워크입니다. 이미지를 주고 개/고양이인지 여부를 판단하거나(classification) 각 픽셀이 어떤 class에 속하는지 판단(image segmentation)을 하는 네트워크 모델을 Discriminator model이라고 합니다.
Discriminator(이하 D)
D는 입력 데이터를 받아서 판단을 하고 출력 데이터를 내보내는 x -> D(x) -> y 구조를 가집니다. 이를 수학적인 관점에서 표현하면 입력 데이터 x에 대하여 label y가 될 조건부 확률 P(y|x)을 구한다고 표현할 수 있습니다.
Generator
반면에 G는 특정한 확률분포 P_{data}(x)를 갖는 학습 데이터를 이용해서 학습을 진행하고, 결과적으로 학습 데이터와 유사한 확률분포 P_{model}(x)를 갖는 데이터를 생성하는 모델입니다. x ~ P_{data}(x) -> G(x) -> y ~ P_{model}(y)
Generative Adversarial Networks?
GAN를 제대로 이해하려면 Generative 와 Adversarial이라는 단어의 의미가 어떻게 네트워크 속에서 표현되고 있는지 확인해야 합니다. 먼저 Generative라는 단어는 기존에는 Discriminator에만 집중되어 있던 모델에 Generator를 추가했다는 의미입니다. Adversarial이라는 말은 G와 D가 서로 대립하면서 적대적으로 학습을 진행한다는 말입니다. 간단히 설명하면 G는 D를 속이기 위해서, D는 G가 만들어낸 가짜 데이터에 속지 않기 위해서 학습을 진행합니다.
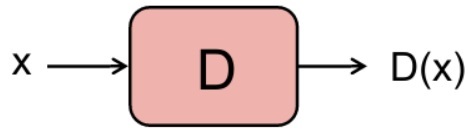
앞서 설명했던 것처럼 D는 입력 데이터 x를 받아서 판단을 하고 출력 데이터 y를 내보내는 역할을 합니다. GAN에서 D의 역할은 입력 데이터 x가 real image같으면 1, 아니면 0을 내보내는 것입니다.
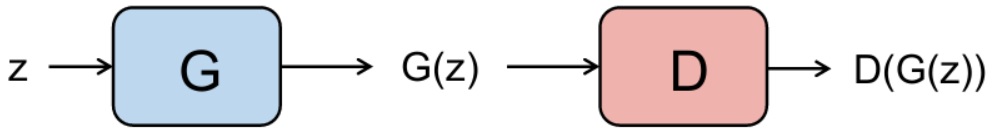
반대로 GAN에서 G의 역할은 임의의 입력 데이터 z를 받아서 fake image를 생성해서 내보내는 것입니다.

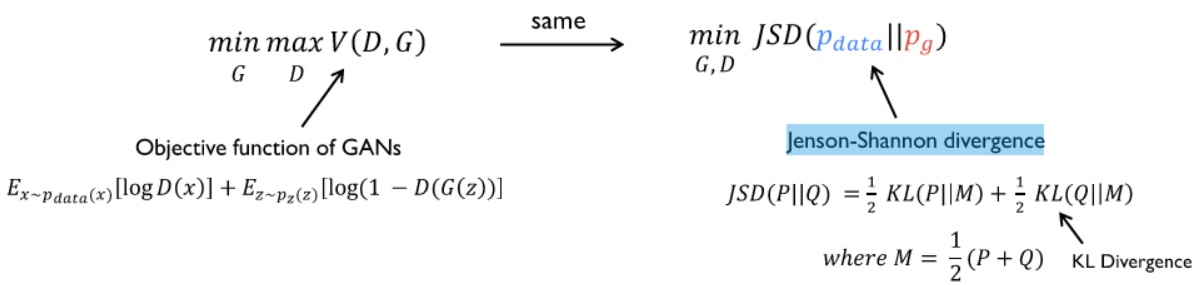
위 식은 GAN의 Loss함수 또는 Objective함수입니다. 먼저 등호 왼쪽에 있는 부분은 “G의 입장에서는, V(G,D)로 표현할 수 있는, 오른쪽 식을 최소화한다.” 그리고 “D의 입장에서는 오른쪽 식을 최대화한다.”입니다. 식에서 P_{data}는 real image에 대한 확률 분포를 의미하고, P_{z}는 G의 입력 데이터로 임의의 값 z를 넣었을 때 출력 이미지의 확률 분포를 의미합니다.
D의 입장에서 먼저 보겠습니다. D(X)는 입력데이터를 real image라고 판단했으면 1, 아니면 0을 출력합니다. 등호 오른쪽 첫 항의 log(D(x))의 x는 real image의 표본 중 하나이기 때문에 D는 D(x)가 1이라고 판단할 확률을 높여야 합니다. 동시에 등호 오른쪽의 두 번째 항의 log(1-(D(G(z))))의 z는 임의의 값이고 G(z)는 fake image를 의미합니다. 따라서 D는 log(1-D(G(z))))의 G(z)를 0이라고 판단할 확률을 높여야 합니다. 결과적으로 첫 항은 log(1)에 수렴하도록, 두 번째 항도 log(1-0)에 수렴하도록 학습을 진행합니다. 위 식에서 왜 E(X)가 나오는지에 대해서는 아래에서 설명하겠습니다.

G의 입장에서는 등호 오른쪽의 첫 장이 필요없습니다. 식에 G(x)가 포함되어 있지 않기 때문입니다. G는 두 번째 항의 D(G(z))가 1을 출력하도록 학습을 진행합니다. 결과적으로 첫 항은 항상 0이고, 두 번째 항은 log(1-1)에 수렴하도록 학습을 진행합니다.
정리하자면 D와 G의 입장에서는 각각 V(D,G)의 값을 최대화/최소화 하는 방향으로 학습을 진행합니다. 서로를 속이기 위해서 적대적으로 학습을 진행하기 때문에 adversarial한 네트워크라고 부릅니다.
GAN Loss 함수의 실질적인 사용 : binary cross entropy
위에서 D는 P(y|x)를 구하는 모델이라고 했습니다. 입력 데이터에 따라서 1 또는 0을 내보내는 기준은 확률입니다. 더 높은 확률을 보이는 결과를 출력합니다. 예를 들어서 입력 데이터의 class가 어떤 것인지 둘 중 하나로 맞춰야하는 경우 ground-truth 확률이 (1.0, 0.0)이라고 할 때, D(x)의 결과는 (0.4,0.6)으로 출력될 수 있습니다. 이 때는 ground-truth 확률에 더 가까워지도록 모델의 parameters를 조정해야 합니다. 여기서 ‘가깝다’라는 기준을 설정하는 방법 중 하나가 binary cross entropy입니다.
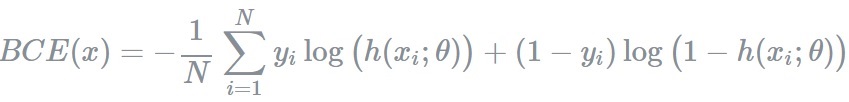
BCE를 이해하기 위한 몇 가지 개념을 리마이인드 하고 넘어가겠습니다.
### 베르누이 분포
어떤 시행을 했을 때 결과가 두 가지 중 하나로만 나오는 실험을 베르누이 시행이라고 합니다. 예를 들어서 동전을 한 번 던지면 앞면 또는 뒷면만 나오기 때문에 이것도 베르누이 시행을 따릅니다. 베르누이 확률변수는 시행의 결과를 1 또는 0으로 바꾼 것을 의미합니다. 확률변수 x가 베르누이 분포를 따른다고 하는 것은
X ~ B(x,p)라고 표현합니다.
위와 같은 정의에 따라서 베르누이 분포를 따르는 X의 기댓값 E(x)는 p입니다.
E[x] = P(x=1) * 1 + P(x=0) * 0 = p * 1 + (1-p) * 0 = p그리고 베르누이 분포를 따르는 x의 분산 V(X)는 p(1-p)입니다.
E[x^2] = P(x=1) * 1^2 + P(x=0) * 0^2 = p * 1^2 + (1-p) * 0^2 = p
V[x] = E[X^2] - (E(x))^2 = p^2 - p = p * (1-p)
### Entropy
엔트로피란 확률적으로 발생하는 사건에 대한 정보량의 평균을 의미합니다. 정보량은 다음과 같이 정의되며 놀람의 정도를 나타낸다고 볼 수 있습니다. 만약 동전을 던져 앞면이 나올 확률은 1/2이기 때문에 I(x)의 값은 log_{2}(2)가 됩니다. 이는 동전을 던지는 사건을 2진수로 표현할 때 최소 1비트가 필요함을 의미합니다. 만약 8가지 선택지가 있는 시행에 대해서는 log_{2}(8) = 3, 즉 3비트가 있어야 8자기 선택지를 모두 표현할 수 있다는 의미입니다. 정리하면,예측이 어려울수록 정보의 양은 더 많아지고 엔트로피는 더 커집니다.
### Cross Entropy
Cross Entropy는 두 개의 확률분포 p와 q에 대해 하나의 사건 X가 갖는 정보량으로 정의됩니다. 즉, 서로 다른 두 확률분포에 대해 같은 사건이 가지는 정보량을 계산한 것입니다. 이는 q에 대한 정보량을 p에 대해서 평균을 구해서 얻을 수 있습니다.
Cross entropy는 기계학습에서 손실함수(loss function)을 정의하는데 사용됩니다. 이때, p는 true probability로써 true label에 대한 분포를, q는 현재 예측모델의 추정값에 대한 분포를 나타냅니다.
### Binary cross entropy Binary cross entropy는 두 개의 class 중 하나를 예측하는 task에 대한 cross entropy의 special case입니다.
다시 돌아와서 이제 왜 GAN의 Loss function에 대해서 더 깊게 이해할 수 있게 되었습니다. 일단 G와 D가 적대적으로 학습하는 것은 알겠는데 왜 E(x)가 등장하는지 이해해보겠습니다. GAN의 D는 input image에 따라서 1 또는 0을 출력합니다. 즉, 두 개의 class 중 하나를 예측하는 task에 대한 cross entropy의 special case인 Binary cross entropy를 사용할 수 있습니다. 위와 같이 Logg Function을 구성해두면, Loss Function을 미분한 기울기만큼 학습이 진행됩니다. 바꿔 말하면 위 Loss Function을 미분하면 cross entopry의 정의에 따라서 예측모델의 추정값의 역(1/ D(G(z)))을 real image의 분포에 따라서 평균을 구한 것입니다. 즉, BCE는 P_{model}과 P_{real}의 확률 분포의 차이를 계산하는 방법이고 이를 각각 최대화/최소화하는 방향으로 학습을 진행합니다.
실제로 아래에서 기술할 GAN tutorial에는 pytorch에서 BCE를 사용하는 코드(nn.BCELoss();)를 보실 수 있습니다. 그런데 프레임워크 내부적으로는 G의 loss function을 아래와 같이 휴리스틱하게 수정해서 사용합니다.

log(1-x)의 x=0일 때 기울기가 너무 작기 때문에 학습 속도를 빠르게 하기 위해서 log(x)를 사용하면서 V(D,G)를 최소화하는 것이 아니라 최대화하는 방향으로 학습을 진행합니다.
학습시키기
일반적인 신경망은 loss function을 정의하고, 오차를 역전파시키면서 변수를 갱신하는 방법을 사용합니다. 특정 목적을 가진 망 1개를 학습시키는 것이기 때문에 지향점이 비교적 명확합니다. 반면에 GAN은 G와 D를 둘 다 학습시키기 때문에 적절한 학습 방법이 필요합니다.
첫 번째 단계는 G를 고정시키고 D를 학습시킵니다. D는 어떤 것이 진짜고 어떤 것이 가짜인지 이미 알고 있기 때문에 일반적인 D의 학습 방법과 동일합니다.
두 번쨰 단계는 D를 고정시키고 G를 학습시킵니다. G는 D를 속이는 방향으로 학습을 진행합니다.
위 두 단계를 반복적으로 수행시키면 D와 G는 발전을 거듭해서 평형상태에 도달합니다.
G model과 maximum likelihood estimation
먼저 이해를 위해 필요한 선행 개념을 익혀보겠습니다.
### likelihood
확률분포가 어떤 분포에 대한 관측 데이터의 확률을 나타낸다면, likelihood 함수는 관측 데이터에 대해 확률 분포의 파라미터가 얼마나 일관되는지를 나타냅니다. 확률 분포 그래프에서 likelihood는 특정 x에 대한 y축 값을 의미합니다.
파라미터 π를 따르는 어떤 확률부포를 f(Y=y;π)라고 할 때, 관측데이터 y에 대한 베르누이 분포는 아래와 같습니다.
f(Y=y;π)=π^{y} * (1−π)^{1−y} ,y∈{0,1}여기서 관측값 y를 고정시키고 위 함수를 π에 대한 함수로 사용한다면 이는 베르누이 분포에 대한 likelihood함수가 됩니다.
L( π ∣ y ) = ∏_{i=1}^{n} f(y_{i} ; π ) , y_{i} ∈ {0,1}, i=1…n
### Loglikelihood
Loglikelihood는 likelihood에 log함수를 취한 형태로 정의되며 종종 계산적 편의를 위해 likelihood 대신 사용됩니다. 한 가지 장점을 예로 들면, log를 씌움으로써 확률의 거듭 곱으로 발생할 수 있는 underflow를 방지할 수 있습니다.
l( π ∣ y ) = log(L( π ∣ y ))
### Maximum Likelihood Estimation
주어진 관측데이터에 대해 likelihood function L(π∣x)를 가장 크게 하는 파라미터 π를 추정하는 것을 maximum-likelihood estimation이라고 합니다.
GAN과 maximum likelihood estimation에 대한 내용을 뒤에서 다시 다룹니다.
### Kullback–Leibler (KL) Divergence
KL Divergence를 통해 두 확률분포 p와 q가 얼마나 다른지를 측정할 수 있습니다.
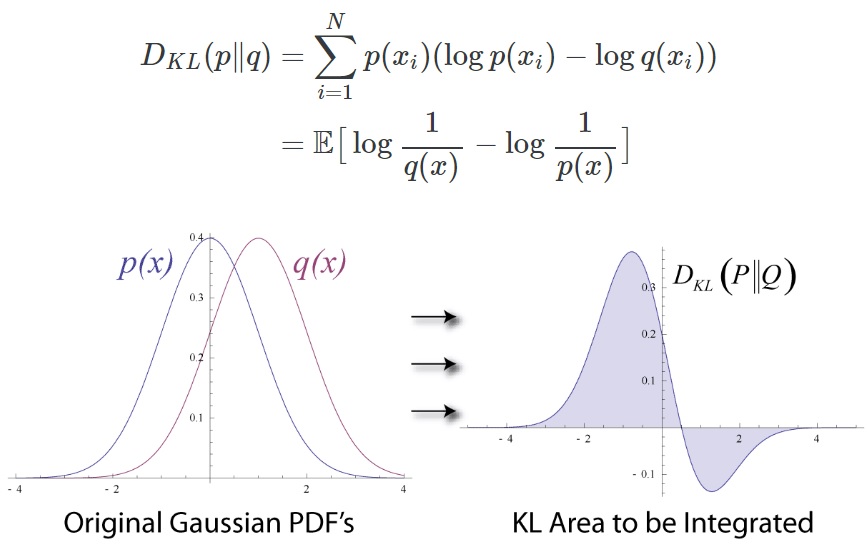
KL 발산은 정보량의 차이에 대한 기댓값입니다. 만약 q가 p를 근사하는 확률분포라면 KL Divergence는 확률분포의 근사를 통해 얼마나 많은 정보를 잃게 되는지를 보여줍니다.
참고로 p와 q의 분포가 동일할 경우, 두 정보량의 차는 0이 되므로 이때 KL Divergence는 0을 반환합니다.
### Jensen-Shannon Divergence
Jensen-Shannon Divergence를 통해 두 확률분포 p와 q가 얼마나 같은지를 측정할 수 있습니다. KLD는 Symmetric하지 않습니다.( D_{KL}(P Q) != D_{KL}(Q P) ) 그래서 KLD를 Symmetric하게 개량한 JSD를 사용합니다.
JSD(p,q) == JSP(q,p)가 되어, 두 확률 분포 사이의 distance로서의 역할을 수 있게 됩니다.
G와 D의 학습을 진행하는 과정에서 P_{model}과 P_{data}의 차이를 줄이는 방향으로 학습을 진행합니다. 이 때 두 확률 분포의 차이를 계산하기 위해서 BCE를 사용하는데 왜 BCE를 사용하는 것이 결과적으로 G,D의 적절한 학습과 동일한 의미인지 알아보겠습니다.
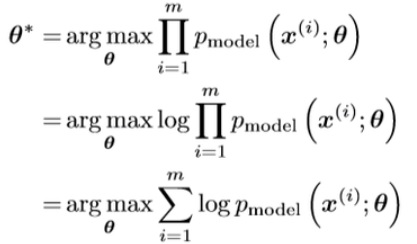
m개의 학습 데이터를 모델 분포에 최적으로 근사시키는 변수 theta를 구하고자 한다면 첫 번째 식처럼, i=[1,m]에 대한 모든 확률의 곱이 최대가 되도록 표현할 수 있습니다. 각각의 확률의 값이 1에 근사한다면 전체의 곱이 최대가 됩니다. 확률의 거듭 곱으로 발생할 수 있는 underflow를 방지하기 위해 Loglikelihood를 사용하고, 식을 재구성하면 엔트로피의 정의 * -1이 됩니다.
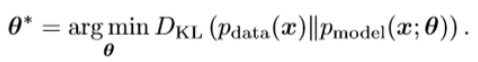
학습 데이터의 분포와 모델 분포를 취적으로 근사시키는 것은 KLD의 최소화시키는 것이고, 이는 다시 JSD를 최소화하는 것이기 때문에 아래식으로 나타낼 수 있습니다.