빠른 속도를 위한 Batch Normalization

Goal : Batch-normalization 머릿 속에서 구체적으로 그릴 수 있다.

Notice:
본 강의는 Coursera의 Andrew Ng의 ML 강의를 요약한 것입니다.

Hyperparameter tuning

Tuning process

우리가 관심을 가져야하는 Hyperparameter들을 정리해보면 아래와 같이 6개가 있습니다.

1. $\alpha$ : Learning rate
2. $\beta$ : Gradient descent with momentum
3. $\beta_1$, $\beta_2$ : Adam optimization algorithm
4. Hidden Layer의 갯수 : Neural Architecture
5. learning rate decay : $\alpha$가 감소하는 정도
6. mini-batch size

이제 이 Hyper들을 어떤 값을 어떻게 고르냐에 따라서 결과에 엄청난 영향을 주기 때문에 이 값들을 잘 고르는 방법을 알아볼 것입니다. 이 과정은 대단히 중요합니다. 예를 들어 mini-batch size를 256에서 512로 올리기만해도 Bias나 variance에서 1%정도의 향상을 얻을 수 있고 이는 아주 대단한 결과입니다.

Info Notice:
GPU Card 4개를 꽂는 GPU Machine은 2000만원, 8개를 꽂는 머신은 1억이라고 합니다. GPU CARD가 비싼 것이 아니라 Work Station이 비싼 것이라고 합니다.

Using an appropriate scale to pick hyperparameters

Picking hyperpatameters at random

$n^l$은 Level이 $l$인 hidden layer의 Node를 의미합니다. 만들고자하는 Architecture에서 $l$을 얼마나 쌓을 것인가? 그리고 각 Layer마다 Node의 갯수 $n$은 몇 개인가?와 같은 문제를 가집니다.

위와 같이 [50,150]에서 랜덤하게 $n^l$의 갯수를 뽑고 싶은데 그냥 랜덤하게 뽑으면 결과가 잘 안 나올 것 같습니다.

Try random values : Don’t use a grid

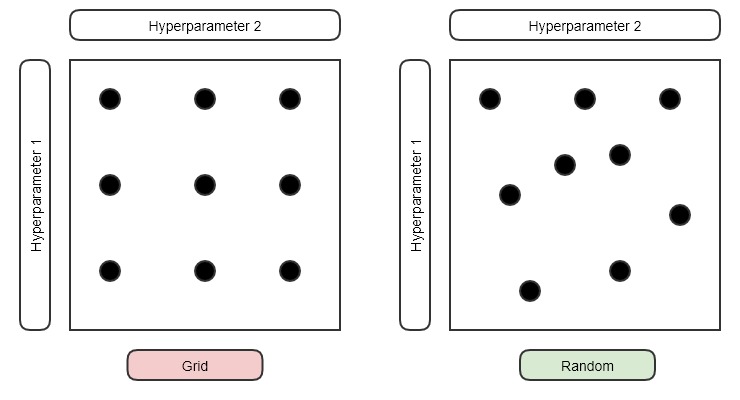
예전에는 grid 방법을 사용했다고 합니다. 두 개의 Hyper를 뽑아야한다고 할 때, 각 Hyper 마다 적절한 후보들을 결정합니다. 그리고 이들의 모든 pairs를 모두 시도해보고 가장 결과가 좋은 방법을 뽑았던 것입니다.

하지만 지금은 Random하게 Hyper를 뽑는 방식 사용합니다. Grid하게 Hyper의 후보들을 선정해두고 진행을 하면 애초에 고려되지 못하는 값들이 너무 많기 때문입니다. 지금은 단순히 2D로 생각했지만 위에서 보았던 것처럼 N-Dimemsion이 되면 커버하지 못하는 부분이 너무 많아집니다.

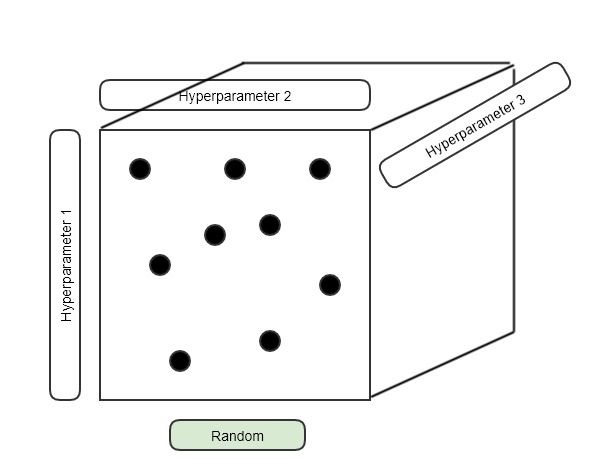
여기서 Grid를 사용하지 말고 random하게 hyper를 pick해야하는 이유는 모든 경우의 수가 나올 가능성이 $\epsilon$(0보다 아주 조금 큰 양수, ML에서는 보통 $10_{-8}$)으로 고려되기 때문입니다.

Coarse to fine

그래도 아직 너무 넓은 범위에서 Random하게 뽑고 있습니다. 일단 적절한 범위에서 Uniform distribution을 통해서 몇 번 시행을 한 뒤에, 가장 좋은 결과를 보이는 일부분의 영억으로 Uniform의 범위를 줄여서 다시 시행을 진행합니다. 이 때 몇 배가 더 빨라지는지/결과가 좋아지는지는 ‘정성적으로만 대략적으로만 직관적으로, 더 좋아진다.’라고만 이해하고 넘어갑니다.

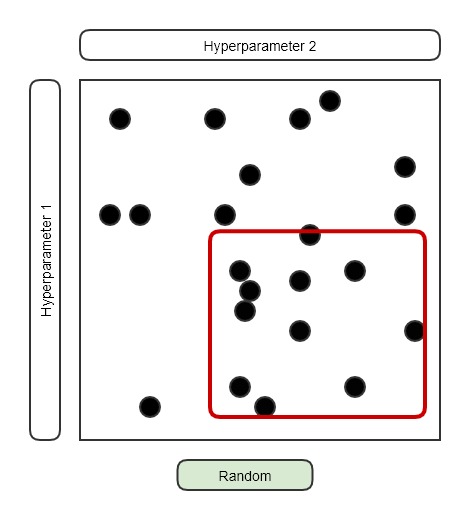
가장 좋은 결과를 보이는 영역이 어디인지 확인하고 해당 부분으로 Uniform의 영역을 좁히는 것은 뒤에서 배울 Mini-batch Normalization의 개념으로 확장됩니다. 매 Mini-batch 마다 exponentially weighted average를 사용해서 평균과 분산을 구하는 과정에서 가능해지는 것입니다. 뒤에서 더 자세하게 다룹니다.

Appropriate scale for hyperparameters

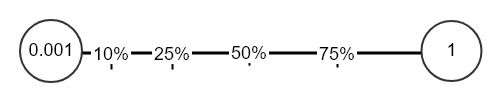
Random하게 Hyper들을 뽑을 때는 그냥 [시작,끝]에서 pick을 하면 안됩니다. 예를 들어서 Learning rate $\alpha$는 보통 굉장히 작은 값을 가지기 때문에 [0.001,1]에서 randomly pick을 합니다. 하지만 경험적으로 1보다는 0.001에 더 가까운 결과를 보일 가능성이 높습니다. 하지만 의외로 0.5의 값에서 좋은 결과를 보일 수도 있으므로 전체 scale을 [0.001,0.4] 따위로 막 좁힐 수는 없는 것입니다. 위 그림에서 아마도 전체 영역의 0~10%되는 영역에서 Hyper가 뽑히는 것이 좋은 결과를 보일 것 같지만 이 영역이 뽑힐 확율은 10%에 불과합니다. 그래서 전체의 범위는 [0.0001,1]이지만 0.0001에 가까울 수록 뽑힐 확률이 높도록 변형을 하고 싶습니다.

이는 $\log$를 사용하면 가능합니다.

Let $\gamma = [a,b]$ $\alpha = 10^{\gamma}$

\[\left\{ \begin{array}{l} a = 0.0001 = 10^{-4} \\ b = 1 \end{array} \right.\]

That is,$\gamma = [0.0001, 1]$

\[\left\{ \begin{array}{l} \log a = -4 \\ \log b = 0 \end{array} \right.\]

Now,$\gamma = [-4, 0]$
$\alpha = [0.0001, 1]$

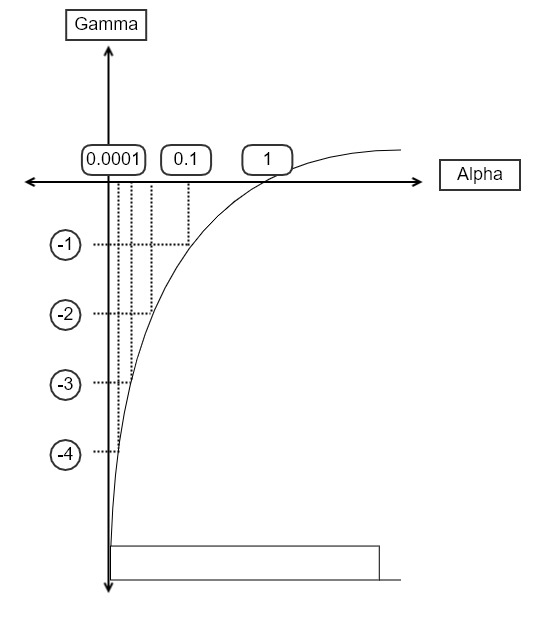
즉, $\alpha$가 [0.0001,0.1] 사이의 값을 가지기 위해서는 $\gamma$가 [-4,-1] 사이의 값을 가지면 됩니다.
$\log$를 취하여 식을 변형한 것이 해당 부분에서 값이 뽑힐 확률을 9.8% 에서 75%까지 끌어올리는 효과를 보였습니다. 여전히 나머지 부분에 대해서도 비례하는 확률을 가집니다.

$\frac{0.1 - 0.0001}{1 - 0.0001} \approx 9.8$
$\frac{-1 - (-4)}{0 - (-4)} = 75%$

이 과정은 아래의 코드로 uniform distribution을 뽑는 것으로 아주 간단하게 표현될 수 있습니다.
np.random.rand() 코드가 [0,1] 사이의 값을 반환하기 때문에 -4를 곱하는 것으로 결과를 [-4,0]에서 uniform하게 뽑힌 결과로 변형시키는 것입니다.

#Create an array of the given shape and populate it with random samples from a uniform distribution over [0, 1).
r = -4 * np.random.rand() 

이렇게 0.0001에 가까운 부분의 확률이 증가된 방향으로 Hyper를 randomly pick할 수 있게 modeling 할 수 있습니다.

마지막으로 [-4,0]의 범위에 %+\alpha%를 하여 임의의 부분에서 uniform distribution을 얻을 수도 있습니다.

Info Notice:
교수님께서 이 부분에서 기말고사 때 한 문제를 출제하실 것 같습니다.

Danger Notice:
입문자들은 이렇게 Random하게 Hyper parameter를 결정하면 안됩니다. 만들고자하는 APP과 관련된 Paper를 보고 이미 사람들이 사용하고 있는 weight와 Hyperparameter를 사용해야합니다.

Paper에는 weights와 Hyperparameters를 어떤 값을 사용했는지 다 나와있습니다. Paper에서 공개되지 않는 내용은 어떻게 학습을 시켰는가?에 관한 내용입니다. 즉, forward-propagation까지는 논문에 다 공개되고 이 값들을 기반으로 시작해야합니다.