[SCPC][2016/5]징검다리 + 개구리 뛰기
문제 : SCPC 2016 징검다리
0번부터 n번까지 번호가 매겨진 징검다리가 있다. 이 다리를 건너는데 오른쪽으로 한 칸부터 k칸까지 건너갈 수 있고, 두 가지 제약 조건이 있다.
- 지뢰가 묻혀진 돌들이 있어서 밟으면 안된다.
- 연속해서 두번 같은 칸을 뛰면 안된다.
이제 n번 돌까지 가는 가짓수를 구하시오.
풀이 : SCPC 2016 징검다리
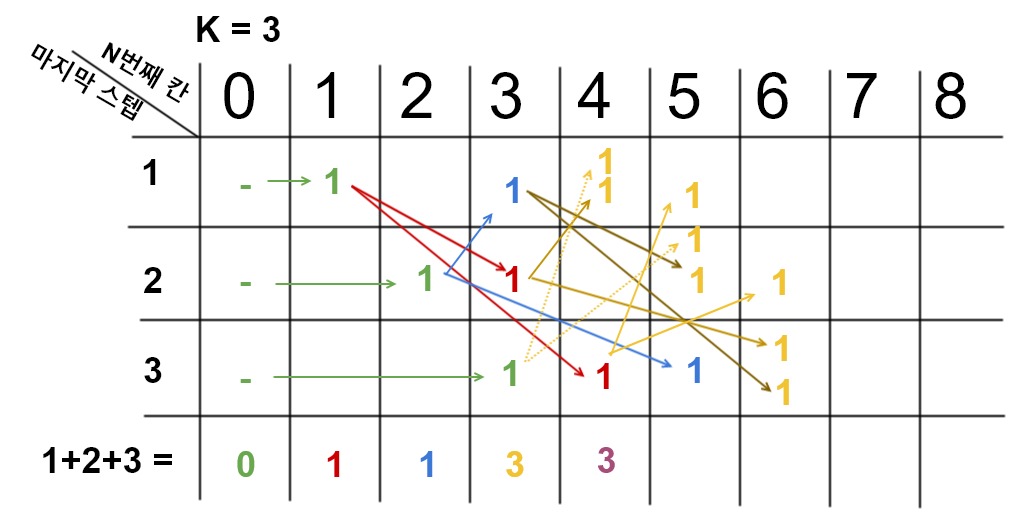
각 칸은 N번째 값에 오기 위해서 밟은 마지막 스텝별로 몇 번의 가능성이 있는지를 나타냅니다. 최종적으로 N번째에 오기 위한 방법은 마지막 스텝이 1,2,3인 경우를 모두 더하면 됩니다. 위 그림에서 1+2+3은 이를 나타냅니다.
- 초록색 : 시작하는 위치 0에서는 아직 아무 것도 적힌 것이 없습니다. 이제 시작 위치에서 갈 수 있는 곳에 1을 적어줍니다.
- 빨간색 : 아무것도 하지 않은 상태에서 1+2+3을 구합니다. 1입니다. 이는 1까지 오는 방법이 1가지 뿐임을 나타냅니다. 1까지 오기 위해서 마지막 스텝이 1인 경우가 1번 있습니다. 이 경우를 생각하면 다음 스텝은 2 또는 3이 될 수 있습니다. 따라서 $dp[현재의값+가능한값][가능한값] += 1$을 해줍니다.
- 파란색 : 아무것도 하지 않은 상태에서 1+2+3을 구합니다. 1입니다. 이는 2까지 오는 방법이 1가지 뿐임을 나타냅니다. 1까지 오기 위해서 마지막 스텝이 2인 경우가 1번 있습니다. 이 경우를 생각하면 다음 스텝은 1 또는 3이 될 수 있습니다. 따라서 $dp[현재의값+가능한값][가능한값] += 1$을 해줍니다.
- 노란색 : 아무것도 하지 않은 상태에서 1+2+3을 구합니다. 3입니다. 이는 3까지 오는 방법이 3가지임을 나타냅니다. 3까지 오기 위해서 마지막 스텝이 1,2,3인 경우가 각각 1번 있습니다. 따라서 각 가능성에 대해서 $dp[현재의값+가능한값][가능한값] += 1$을 해줍니다.
- 보라색 : 아무것도 하지 않은 상태에서 1+2+3을 구합니다. 3입니다. 이는 3까지 오는 방법이 3가지임을 나타냅니다. …
- 원하는 N까지 도달할 떄까지 위 알고리즘을 반복합니다.
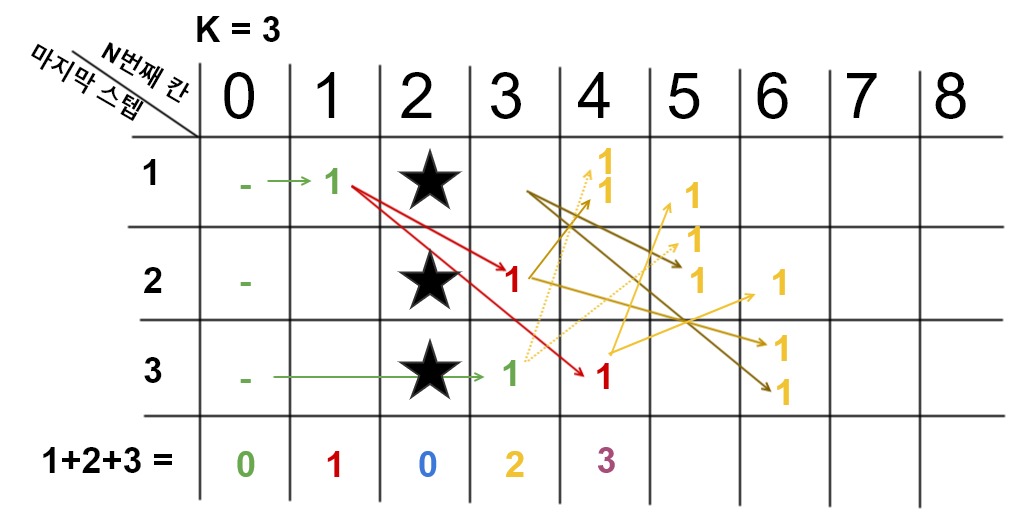
- 문제에서는 지뢰가 묻혀진 돌들을 밟으면 안된다고 했습니다. 만약에 지뢰가 2에 있다면 아래와 같은 모습일 것입니다.
코드 : SCPC 2016 징검다리
알고리즘은 이정도로 된 것 같습니다. 기말고사가 끝나면 코드로 옮겨봐야겠습니다.
문제 : SCPC 2015 개구리 뛰기
일직선 상에 돌들이 있고, 개구리가 처음 좌표 0에 있다. 좌표 0에는 항상 돌이 있다. 개구리가 최대 K칸 뛸 수 있을 때, 가장 마지막 돌에 도착할 수 있다면 최소 점프 수를 구하시오.
예를 들어, 돌이 0, 1, 2, 5, 7, 9, 10, 12, 15에 있고 개구리가 최대 K=4칸 뛸 수 있다면 0-2-5-9-12-15, 총 5번 점프해서 뛸 수 있다. 반면 K=2칸 뛸 수 있다면 개구리는 2번 돌 이후로 갈 수 없으므로 이동할 수 없다.
풀이 : SCPC 2015 개구리 뛰기
그리디로 풀면 됩니다. 즉, 그 때 그 떄 제일 멀리 뛰어보고 끝까지 도달할 수 없다면 불가능합니다.
돌이 0, 1, 2, 6, 7, 9, 10, 12, 15에 있을 때 K=3이라고 해보겠습니다. 이 때 0에서 갈 수 있는 제일 먼 2까지 갑니다. 다음에는 K칸을 뛰어도 다음으로 갈 수 없습니다. 여기까지만 확인해도 더이상 진행할 수 없는 것을 알 수 있습니다. 1부터 K칸을 뛰었을 떄 갈 수 있는 가장 먼 돌이 하나도 없을 때, 1부터 K보다 적은 칸을 뛰었을 때 갈 수 있는 돌이 생기는 경우는 없기 때문입니다.
코드 : SCPC 2015 개구리 뛰기
알고리즘은 이정도로 된 것 같습니다. 기말고사가 끝나면 코드로 옮겨봐야겠습니다.
