[SCPC][2015][예선] 1번 MT 문제
간략히 정리한 문제
A, B 두 과 사람들이 다음과 같은 게임을 한다. A과의 학생은 a명, B과의 학생은 b명이다. N, K가 주어졌을 때 다음과 같은 게임을 한다. 1부터 시작해서 모든 학생은 1~k 개의 연속한 숫자를 부를 수 있다. A과가 먼저 시작하고 A과의 모든 학생이 자신이 정한 숫자(1~k)개의 수를 부른 후 B과의 학생이 같은 방법으로 진행한다. N을 부르는 학생이 속한 과가 진다.
- N, K가 주어졌을 때 어느 과가 이기는지 구하시오. $1≤b≤a≤10,000$ , $2≤N≤1,000,000$, $1≤K≤1,000$ 이다.
- 전체 수행 시간은 3초 이내. (Java 4초 이내)
45점 풀이
31 게임의 반드시 이기는 알고리즘을 변형한 풀이입니다. A과와 B과가 진행하는 게임을 a과 대표 1명과 b과 대표 1명이 진행하는 게임으로 변형합니다. 그리고 이들이 각각 부를 수 있는 수의 갯수는 A과 대표는 a~ak B과 대표는 b~bk개 입니다.
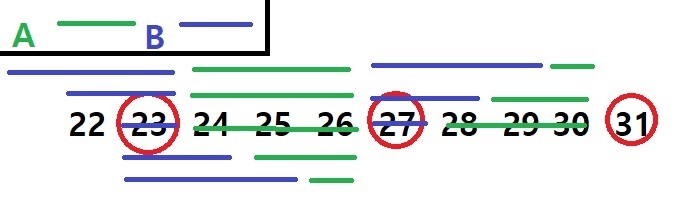
A와 B는 숫자 3개씩을 부를 수 있습니다. A가 먼저 시작해서 반드시 이기기 위해서는 27을 B가 부르게 만들면 됩니다. B가 어떤 갯수의 숫자를 말해도, A는 숫자의 합이 4가 되도록 부를 수 있습니다. 즉, A는 B가 31을 부르게 만들기 위해서 27을 부르게하고, 27을 부르게 하기 위해서 23을 부르게 합니다. 결국 31에서 4를 계속 빼서 B가 3불러야하는 상황을 만들 수 있습니다. A는 1,2까지만 말하면 B는 그 순간 졌다고 볼 수 있습니다.
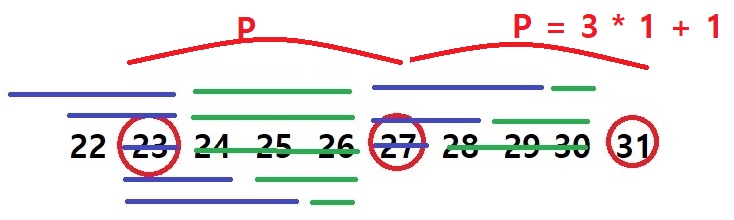
왜 합이 4가 되게 만들어야하는지는 다음 그림을 보면 알 수 있습니다.

MT 문제를 읽고 오면 위 그림을 이해할 수 있습니다. 위 그림에서의 P가 31 게임에서의 숫자 4에 해당합니다. 즉, A의 입장에서 B가 부른 숫자와 내가 부를 숫자의 갯수의 합과 일치시켜야 하는 값입니다. 하지만 이 알고리즘을 코드로 옮기면 아래와 같고 부분점수 45점만 받을 수 있습니다. 왜일까요?
두 명이 부르는 수의 합이 7이 되도록 조절하는 것은 위 그림에서 가능했습니다. 두 번 째 경우(2)의 경우 p = 2 + 3 * 2 = 8인데, 두 명이 부르는 수의 합을 8로 조절하는 것도 가능합니다. 또 하나의 P를 만들 수 있다는 것은 B가 밟았을 때 반드시 A가 이기는 폭탄을 하나 더 만드는 것으로 생각할 수 있습니다. 모든 P를 고려하지 않는다면, A가 이기는 조건 중에 일부만 구하는 것이므로 부분점수만 받을 수 있습니다.
예를 들어서 a=2, b=2=1, k=3일 때 가능한 P는 5,6,7입니다.
- N이 8일 때, 8%5, 8%6, 8%7, 즉 3, 2, 1 위치에도 폭탄을 놓을 수 있습니다. 이 폭탄을 B가 밟는 순간 A가 두 명이 부르는 수의 갯수를 P개로 조절해서 A가 이깁니다.
- N이 9일 때, 폭탄이 4,3,2 위치에 추가됩니다. 이 중에 하나라도 B가 밟게 만들 수 있다면 A는 이길 수 있습니다.
- N이 10일 때, 폭탄이 5,4,3 위치에 추가됩니다. 이 중에 하날도 B가 밟게 만들 수 있다면 A는 이길 수 있습니다.
만약 A가 폭탄을 밟는 경우, B는 이에 대응하는 P로 두 명이 부르는 숫자의 갯수를 맞출 것이고, B가 이길 것입니다. 그래서 A가 자신이 설치한 폭탄을 피할 수 있는지 없는지 판단해야 합니다. a,b,k가 주어졌을 때 가능한 P 갯수는 최대 - 최소 = (b+ak) - (a+bk) = (a-b)(k-1)개 입니다. 주어진 N에 따라서 (a-b)(k-1)개의 폭탄의 위치를 판별하고, 이 폭탄이 재수없게 a가 움직일 수 있는 a~ak의 범위를 모두 커버한다면 A가 질 수밖에 없습니다.
범위를 모두 커버하는지 판단하기 위해서는 a~ak의 갯수 ak-a+1과 (a-b)(k-1)를 비교해야합니다. 전자가 더 많다면 A가 갈 수 있는 경로가 더 많은 것이므로 A는 자신이 설치한 폭탄을 피할 수 있고, A가 이깁니다. 전자와 후자가 같거나 후자가 더 크면 일일이 비교해서 A의 모든 경로를 덮는지 판단해야 합니다. 이는 폭탄의 위치를 하나씩 판단해보고 마지막으로 a가 갈 수 있는 모든 길이 모두 막혔는지 훑어보면 됩니다. 즉 $O((a-b)(k-1) + (ak-a+1))$만에 할 수 있습니다.
이정도 생각하는데 이 문제에만 10시간은 쓴 것 같습니다. 이렇게 모든 경로를 가능성을 다 판단하고(다 판단한 건지도 모르겠네요.) 코드까지 짜는 것은 불가능해 보입니다. 그래서 똑똑하게 아래와 같이 DP로 풀어야 합니다.
DP : 이인복 교수님 + 최백준 + 장환석 풀이
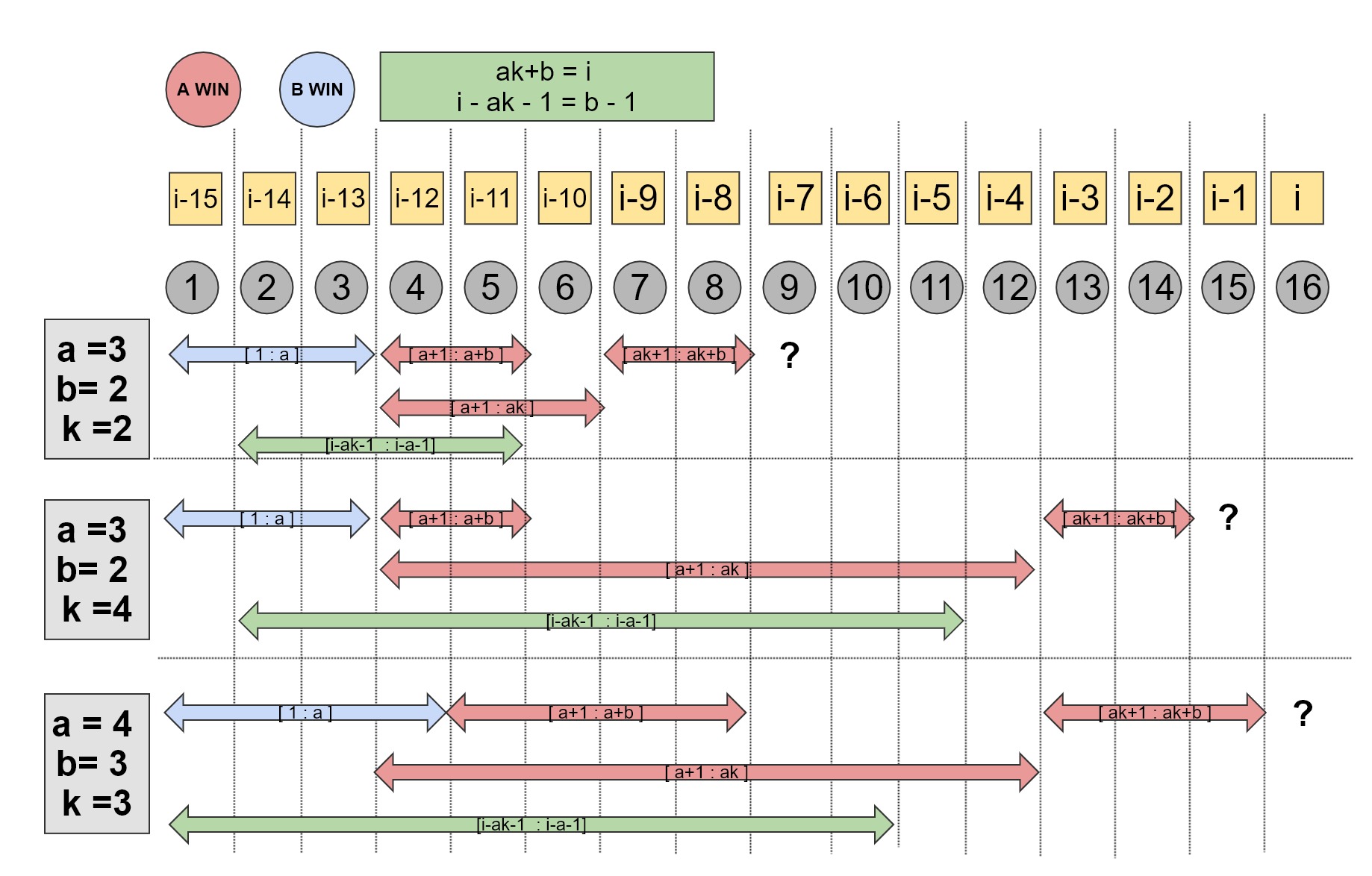
- $[1:a]$ : A가 반드시 불러야하는 숫자입니다. 이 범위에 N이 있다면 B WIN입니다.
- $[a+1 :a+b]$ : A가 최소로 a개만 부르고 멈추면 B는 자신의 최소 갯수 b 개를 채우다가 N을 불러야합니다. A가 반드시 WIN 하는 구역입니다.
- $[ak+1 : ak+b]$ : A가 최대로 ak개 부르고 멈추면 B는 자신의 최소 갯수 b 개를 채우다가 N을 불러야합니다. A가 반드시 WIN 하는 구역입니다.
- $[a+1 : ak]$ : 또는 $[a+1 : ak+1]$ : A가 부르는 갯수를 조절해서 B가 반드시 다음 숫자를 부르게 만들 수 있음으로 A WIN 구역입니다.
- $[i-ak-1 : i-a-1]$ : 1.~4.의 체크가 끝난 뒤에 이들을 사용해서 ? 위치에서 A가 이기는지 B가 이기는지 판단할 수 있습니다. 설명은 아래 그림 입니다.
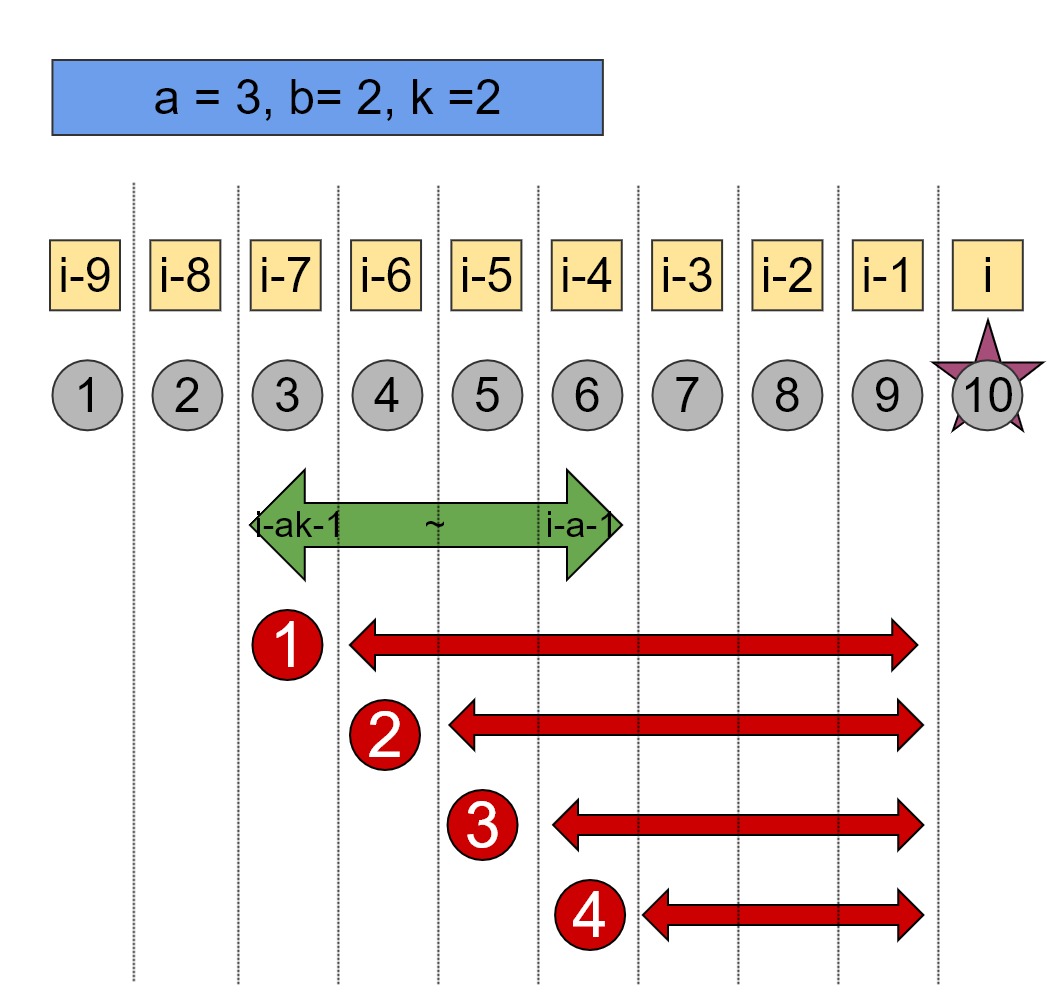
10번째에 폭탄이 있다면 $[i-ak-1 : i-a-1]$ 중 한 군데에서라도 B가 숫자 부르는 것을 멈추면 A가 9번까지 불러서, B가 10을 부르도록 유도할 수 있음을 나타내는 그림입니다. 따라서 $[i-ak-1 : i-a-1]$에서 하나라도 B가 부를 수 밖에 없는 경우(B LOSE 또는 A WIN)이 있다면 10번 째는 A가 이깁니다.

DP : 시간 복잡도 $O(NK)$
모든 dp[i]를 구하기 위해서 $[i-ak-1 : i-a-1]$ 범위의 $a(k-1)$ 개를 판단해야 하므로 $O(NAK)$가 걸립니다. 위 그림의 $O(NK(a+b))$는 어떻게 생각한건지 모르겠습니다.
DP : 시간 복잡도 $O(N)$
최백준님의 풀이를 들어보면 시간복잡도를 $O(NK)$까지 줄이십니다. “1:04:08”부터 보면 이해할 수 있습니다.
이 문제를 이해하기 위해서는 돌게임 문제를 풀어봐야한다는데.. 방학에 풀어보겠습니다.
45점 코드 :
아래의 코드는 제일 작은 P 1개의 가능성만 판단했기 때문에 45점밖에 받지 못했습니다. 모든 가능한 P를 확인하는 코드는 방학에 올리겠습니다.
#include <iostream>
#include <string>
using namespace std;
string Answer = "";
int main(int argc, char** argv)
{
int T, test_case;
//freopen("input.txt", "r", stdin);
cin >> T;
int a = 0, b = 0, c = 0;
for (test_case = 0; test_case < T; test_case++)
{
cin >> a >> b >> c;
//scanf_s("%d %d %d", &a, &b, &c);
int n = 0, k = 0;
for (int i = 0; i < c; i++) {
cin >> n >> k;
int p = 0;
bool flag = false;
for (p = b * k + a; p <= b + a * k; p++) {
n %= p;
if (a > n) n += p;
if (n > a) {
if (Answer == "") {
Answer = "a";
flag = true;
break;
}
else {
Answer += "a";
flag = true;
break;
}
}
}
if (flag == false) {
if (Answer == "") {
Answer = "b";
}
else {
Answer += "b";
}
}
}
cout << "Case #" << test_case + 1 << endl;
cout << Answer << endl;
Answer = "";
}
return 0;
}
백준 풀이
- 참고문제 :프로돌게이머-시리즈
