BFS 문제 풀이 - 1
Goal : 최단거리 알고리즘으로서의 BFS를 내 손이 멋대로 짜게 한다.
개념
BFS는 임의의 정점에서 모든 정점을 한 번씩만 방문하는 알고리즘입니다. 이런 BFS가 아래의 조건일 때는 최단거리 알고리즘으로 사용됩니다.
모든 가중치가 1일 때
BFS를 이용해서 해결할 수 있는 문제의 조건
- 최소 비용의 문제이어야 한다.
- 간선의 가중치가 1이어야 한다.
- 정점과 간선의 갯수가 적어야 한다. (적다는 것은 문제의 조건에 맞추어서 해결할 수 있을 정도로 작다라는 의미)(시간 제한 + 메모리 제한)
즉, 최소 비용의 의미가 간선의 가중치를 의미해야 합니다.
백준 2178번 : 미로 탐색
문제
(1,1)에서 (N,M)으로 가는 가장 빠른 길을 구하는 문제.
풀이
가장 빠른 길은 방문한 칸의 수가 제일 적은 것을 의미합니다.
- x와 y 혹은 w와 h의 좌표를 헷갈리면 안됩니다.
- queue를 queue<pair<int,int» type으로 선언해야합니다.
- queue.front의 pair를 사용해서 다름 BFS의 depth를 계산해야합니다.
코드
/*
2019-05-06
장환석
문제
N×M크기의 배열로 표현되는 미로가 있다.
1 0 1 1 1 1
1 0 1 0 1 0
1 0 1 0 1 1
1 1 1 0 1 1
미로에서 1은 이동할 수 있는 칸을 나타내고, 0은 이동할 수 없는 칸을 나타낸다. 이러한 미로가 주어졌을 때, (1, 1)에서 출발하여 (N, M)의 위치로 이동할 때 지나야 하는 최소의 칸 수를 구하는 프로그램을 작성하시오. 한 칸에서 다른 칸으로 이동할 때, 서로 인접한 칸으로만 이동할 수 있다.
위의 예에서는 15칸을 지나야 (N, M)의 위치로 이동할 수 있다. 칸을 셀 때에는 시작 위치와 도착 위치도 포함한다.
입력
첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.
출력
첫째 줄에 지나야 하는 최소의 칸 수를 출력한다. 항상 도착위치로 이동할 수 있는 경우만 입력으로 주어진다.
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
int N, M;
int a[100][100];
using namespace std;
queue<pair<int,int>> q;
int check[100][100];
// 상 하 좌 우
/*
|
----+---------------> x 축
|(0,0) (0,1),(0,2)
|(1,0) (1,1),(1,2)
y축
*/
int dx[4] = { 0,0,-1,+1 };
int dy[4] = { 1,-1,0,0 };
void dfs(int i, int j, int &count) {
check[i][j] = count;
//printf("push %d %d\n", i, j);
q.push(make_pair(i,j));
while (!q.empty()) {
pair<int,int> curr = q.front(); q.pop();
int nx = 0, ny =0;
for (int k = 0; k < 4; k++) {
nx = curr.first + dx[k];
if (nx < 0 || nx >= N) continue;
ny = curr.second + dy[k];
if (ny < 0 || ny >= M) continue;
if (a[nx][ny] == 1 && check[nx][ny] == 0) {
check[nx][ny] = check[curr.first][curr.second]+1;
//printf("push %d\n",a[nx][ny]);
q.push(make_pair(nx, ny));
}
}
}
}
int main(void) {
scanf("%d %d", &N, &M);
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
scanf("%1d", &a[i][j]);
}
}
int count = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if(a[i][j] == 1 && check[i][j] == 0) dfs(i, j, ++count);
}
}
printf("%d",check[N - 1][M - 1]);
return 0;
}
백준 7576 문제 토마토
풀이 :
- 전체를 한 번 돌면서 bfs를 시작해야하는 지점을 모두 q에 다 넣고 시작합니다.
- 한번 pop할 때마다 pop된 값에서 근처에 있는 값들 중 안익었다가 익게된 토마토를 다시 q에 넣습니다.
/*
2019-03-21
장환석
문제
철수의 토마토 농장에서는 토마토를 보관하는 큰 창고를 가지고 있다. 토마토는 아래의 그림과 같이 격자 모양 상자의 칸에 하나씩 넣어서 창고에 보관한다.
창고에 보관되는 토마토들 중에는 잘 익은 것도 있지만, 아직 익지 않은 토마토들도 있을 수 있다. 보관 후 하루가 지나면, 익은 토마토들의 인접한 곳에 있는 익지 않은 토마토들은 익은 토마토의 영향을 받아 익게 된다. 하나의 토마토의 인접한 곳은 왼쪽, 오른쪽, 앞, 뒤 네 방향에 있는 토마토를 의미한다. 대각선 방향에 있는 토마토들에게는 영향을 주지 못하며, 토마토가 혼자 저절로 익는 경우는 없다고 가정한다. 철수는 창고에 보관된 토마토들이 며칠이 지나면 다 익게 되는지, 그 최소 일수를 알고 싶어 한다.
토마토를 창고에 보관하는 격자모양의 상자들의 크기와 익은 토마토들과 익지 않은 토마토들의 정보가 주어졌을 때, 며칠이 지나면 토마토들이 모두 익는지, 그 최소 일수를 구하는 프로그램을 작성하라. 단, 상자의 일부 칸에는 토마토가 들어있지 않을 수도 있다.
입력
첫 줄에는 상자의 크기를 나타내는 두 정수 M,N이 주어진다. M은 상자의 가로 칸의 수, N 은 상자의 세로 칸의 수를 나타낸다. 단, 2 ≤ M,N ≤ 1,000 이다. 둘째 줄부터는 하나의 상자에 저장된 토마토들의 정보가 주어진다. 즉, 둘째 줄부터 N개의 줄에는 상자에 담긴 토마토의 정보가 주어진다. 하나의 줄에는 상자 가로줄에 들어있는 토마토의 상태가 M개의 정수로 주어진다. 정수 1은 익은 토마토, 정수 0은 익지 않은 토마토, 정수 -1은 토마토가 들어있지 않은 칸을 나타낸다.
출력
여러분은 토마토가 모두 익을 때까지의 최소 날짜를 출력해야 한다. 만약, 저장될 때부터 모든 토마토가 익어있는 상태이면 0을 출력해야 하고, 토마토가 모두 익지는 못하는 상황이면 -1을 출력해야 한다.
*/
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
int M, N;
int a[1000][1000];
// 상 하 좌 우
int dh[] = { -1,1, 0, 0 };
int dw[] = { 0,0, -1, 1 };
queue<pair<int, int>> q;
int day = 0;
void bfs(void) {
int nw = 0, nh = 0;
while (!q.empty()) {
//하나 뽑고
pair<int,int> curr = q.front(); q.pop();
//사방 넣고
for (int k = 0; k < 4; k++) {
//index 예외처리
nh = curr.first+ dh[k];
if (nh < 0 || nh >= N) continue;
nw = curr.second+ dw[k];
if (nw < 0 || nw >= M) continue;
//안익었으면 익히고 day++
if (a[nh][nw] == 0) {
a[nh][nw] = a[curr.first][curr.second] + 1;
if (day < a[curr.first][curr.second] + 1) day = a[curr.first][curr.second] + 1;
q.push(make_pair(nh, nw));
}
}
//다시 뽑고
}
}
int main(void) {
bool noZero = true; //모든 토마토가 익어있는 상태 : 0이 하나도 없는 상태이면 false 아니면 true
scanf("%d %d", &M, &N);
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
scanf("%d", &a[i][j]);
if (a[i][j] == 0){
noZero = false;
}
}
}
//모든 토마토가 익어있는 상태면
if (noZero) {
printf("0\n");
return 0;
}
//전체를 돌면서 step1에서 안익은 토마토를 q에 다 넣는다
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if (a[i][j] == 1) {
q.push(make_pair(i, j));
}
}
}
bfs();
//익지 못하는 경우가 있으면
bool isAllNotRippable = false;
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if (a[i][j] == 0) isAllNotRippable = true;
}
}
if (isAllNotRippable) {
printf("-1\n");
}
else {
printf("%d\n", day-1);
}
return 0;
}
1697번 숨바꼭질 1
풀이 :
BFS를 이용해서 해결할 수 있는 문제의 조건을 모두 만족하므로 BFS 문제입니다.
- 최소 비용의 문제이어야 한다.
- 간선의 가중치가 1이어야 한다.
- 정점과 간선의 갯수가 적어야 한다. (적다는 것은 문제의 조건에 맞추어서 해결할 수 있을 정도로 작다라는 의미)(시간 제한 + 메모리 제한)
N부터 시작해서 N+1, N-1, 2N의 세 방향으로 BFS를 진행한다고 생각하면 됩니다. 주의할 점은 행렬의 길이가 2N을 커버하기 위해서 200,000이 되어야한다는 점입니다. 그리고 마지막 출력은 check[K]를 통해서 바로 할 수 있습니다.
아래의 코드에서 check의 값 0은 아직 방문하지 않았음을, N은 N초 후에 도달할 수 있음을 의미합니다.
/*
2019-05-08
장환석
숨바꼭질
시간 제한 메모리 제한 제출 정답 맞은 사람 정답 비율
2 초 128 MB 52572 14518 8972 24.719%
문제
수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 100,000)에 있고, 동생은 점 K(0 ≤ K ≤ 100,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일 때 걷는다면 1초 후에 X-1 또는 X+1로 이동하게 된다. 순간이동을 하는 경우에는 1초 후에 2*X의 위치로 이동하게 된다.
수빈이와 동생의 위치가 주어졌을 때, 수빈이가 동생을 찾을 수 있는 가장 빠른 시간이 몇 초 후인지 구하는 프로그램을 작성하시오.
입력
첫 번째 줄에 수빈이가 있는 위치 N과 동생이 있는 위치 K가 주어진다. N과 K는 정수이다.
출력
수빈이가 동생을 찾는 가장 빠른 시간을 출력한다.
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
int N, K;
int check[200000]; //0은 방문하지 않음. 시작은 1 다음 step은 2 ~~~ 총 step 갯수는 최대값 -1
int bfs(int start) {
queue<int> q;
check[start] = 1;
q.push(start);
int temp = 0;
while (!q.empty()) {
int curr = q.front(); q.pop();
temp = curr * 2;
if (0 <= temp && temp < 200000) {
if (check[temp] == 0) {
check[temp] = check[curr] + 1;
q.push(temp);
}
}
temp = curr + 1;
if (0 <= temp && temp < 200000) {
if (check[temp] == 0) {
check[temp] = check[curr] + 1;
q.push(temp);
}
}
temp = curr - 1;
if (0 <= temp && temp < 200000) {
if (check[temp] == 0) {
check[temp] = check[curr] + 1;
q.push(temp);
}
}
}
return -1;
}
int main(void) {
scanf("%d %d", &N, &K);
bfs(N);
printf("%d\n",check[K]-1);
return 0;
}
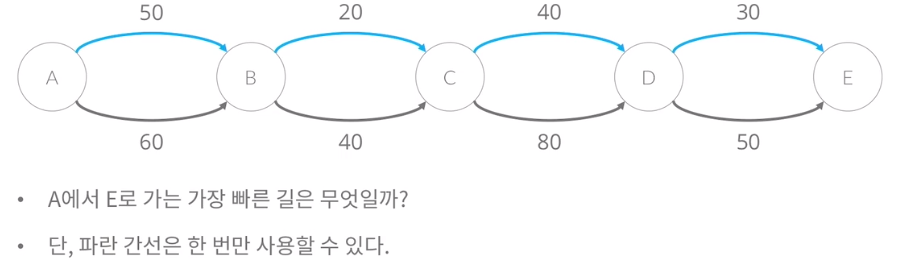
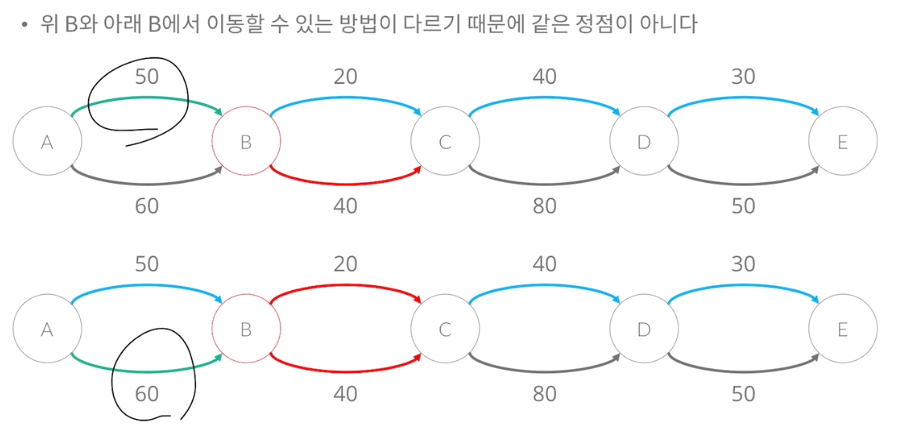
위 B와 아래의 B가 다르다고 한 기준은 파란 간선의 사용한 횟수입니다. 따라서 정점을 파란 간선을 사용한 횟수로 나눌 수 있다.
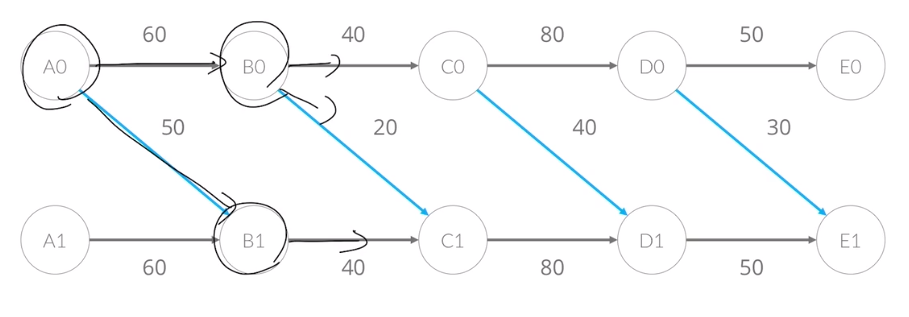
파란 간선을 한 번 사용하면 X1의 노드로만 움직일 수 있는 그래프를 의미합니다.
백준 14226 이모티콘
풀이 :
queue를 만들 때 pair<int,int> type으로 만드는데 앞의 int는 현재 screen에 적혀있는 이모티콘의 수, 뒤의 int는 클립보드에 저장되어 있는 이모티콘의 수를 나타냅니다.
코드에서 보이는 것처럼 3가지의 모든 경우에 대해서 push를 하고 BFS를 돌리면 됩니다. 이 떄 주의할 점은 현재 스크린에 하나의 이모티콘이 적혀있어도, 클립보드에 저장되어있는 이모티콘의
수에 따라서 다른 상태로 본다는 점입니다.
check 배열은 방문하지 않았으면 0, 최초 방문은 1, 다음 방문은 이전에 방문했던 Node의 check + 1이 저장됩니다.
curr.first + curr.second <= S 코드는 현재 screen에 적혀있는 이모티콘의 수와 클립보드에 저장되어 있는 이모티콘의 수의 합이 S를 넘지 않게해줍니다.
혹은 index가 배열의 범위를 넘어가서 runtime error가 나지 않도록 해줍니다.
check[i][j]에서 J의 상한은 i와 j가 pair로써 1대1 대응되기 때문에 i와 j의 상한이 같습니다. 더 정확하게는 부여된 의미에 따라서 j는 i의 상한과 같습니다.
이제 i의 상한을 결정해야합니다. 결론부터 말하면 문제에서 S의 상한이 i의 상한이 됩니다. 만약 입력되는 S의 최대값이 3이라면 queue에는 (4,0) (4,1) 등의 (4,*)값을 저장(체크)할 필요가 없기 때문입니다.
조금 더 자세히 보겠습니다. queue에 push되는 pair를 (s,c)라고할 때, c는 이전 c의 값을 그대로 유지하거나, s의 값을 가져올 수밖에 없습니다. 그런데 이전의 c값도 이전이전의 값을 그대로 갖고 있거나 s의 값을 가져올 수밖에 없습니다. 따라서 $1<= c <= S$라는 범위가 나옵니다. 그러면 현재 (s,c)라는 pair를 가지고 있을 때 s가 제일 빨리 커질 수 있는 방법은 (s,c) => (s,s) -> (s+s, s)입니다. 즉 가중치 1과 1을 지나서 s를 2배로 만드는 방법이 제일 빠르게 s를 증가시키는 방법입니다.
우리는 (1,0)에서 시작해서 (s,)까지 가고 싶습니다. 앞의 숫자가 s면 뒤의 숫자가 0이든 1이든 상관없습니다. (s,) pair가 딱 구해질 때까지만 진행할 것이기 때문입니다. 그래서 (s,) 이후에 (s,s) / (s+, ) / (s-1, *) 으로의 진행을 진행하지 않습니다. 그런데 생각해보면 (s,)가 될 수 있는 방법은 아래와 같은 경우뿐입니다.
- (s’,) -> (s’+ , ) = (s,) // E.g. ( s/2 , * ) -> (s/2,s/2) -> (s, s/2)
- (s+1, ) -> (s,)
그런데 2번의 경우는 불가능합니다. 왜냐하면 s를 구하기 위해서 s+1를 먼저 구한다는 방법인데, s보다 큰 수를 s+1보다 빨리 구할 수는 없기 떄문입니다.
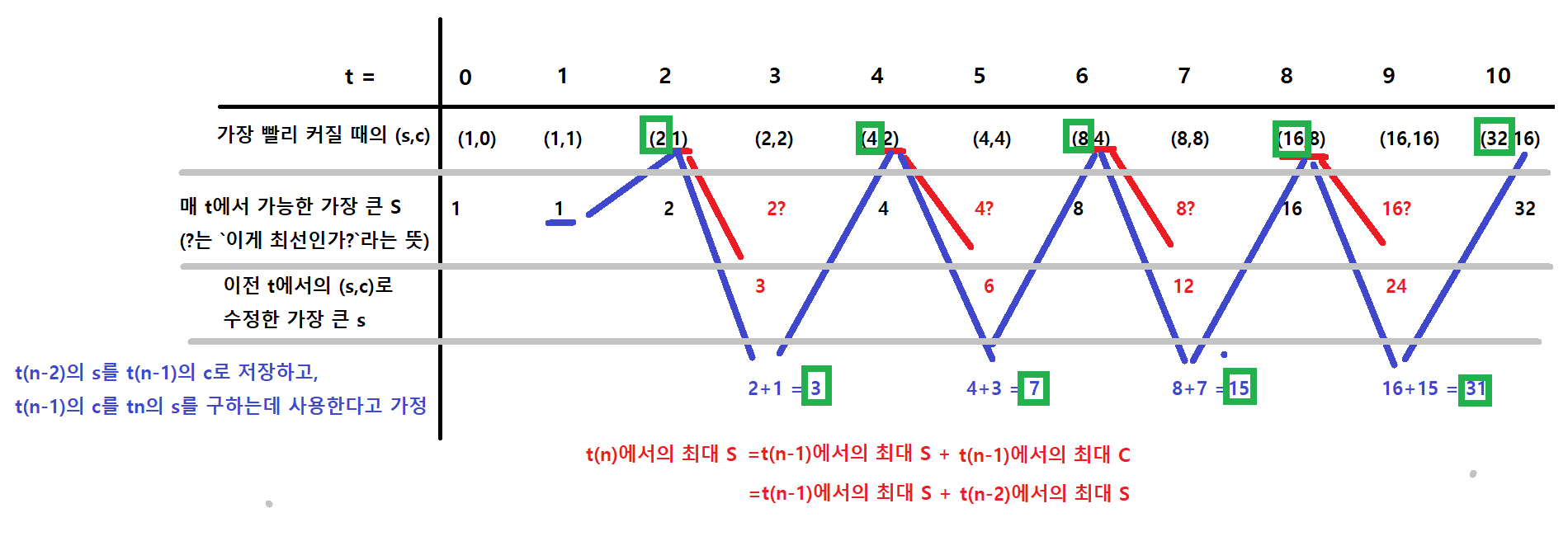
그림 설명은 다음과 같습니다.
- 가장 빨리 S를 키우는 방법은
클립보드에 전체를 저장 -> 붙혀넣기를 반복하는 행위입니다. - 이렇게 구하면 2,4,6,8,10 ~ 번째에서 2배씩 커지는 s를 구할 수 있습니다.
- 하지만 3,5,7,9에서는 현재 구한 s보다 더 큰 s를 구할 수 있을 것 같습니다.
- 빨간색 선을 보면, 이전 t의 s,c를 더해서 현재 t의 s를 구하는 것이 (붙혀넣기) 3,5,7,9번째 시도에서 가장 큰 s를 구할 수 있는 것으로 보입니다.(아직 확실하지는 않음)
- 파간색 선을 보면, 4번에서 구한 답보다 더 확실하게 3,5,7,9에서 가질 수 있는 가장 큰 s를 구하기 위해서는 이전 t의 s와 c를 더하는 것인데, 이전 t의 최대 값은 2번에서 구한 값이 확실합니다. 따라서 이전-이전 t의 s를 이전 t의 c로 옮긴 뒤, 이전 t의 s와 c를 더해서 현재 t의 s의 가장 큰 s가 될 것입니다. 이렇게 구한 3,5,7,9의 s는 사실 불가능한 값일 수도 있습니다. 굵은 글씨로 표시한 부분이 가능한지 증명이 되지 않았기 때문입니다. 하지만 이렇게까지 아마도 불가능한 경우의 가능성까지 포함했을 때도 안되면, 실제로 가능한 경우만 따져 봤을 때는 분명히 안될 것이다. 라는 논리를 사용하겠습니다.
- 초록색 네모를 보면, 5번에서 수정한 각 t에서의 최대 s를 순서대로 보면 계속 오름차순입니다. 즉, S가 t번째에서 구해진다고 했을 때, S보다 큰 수를 t-1번째에서 먼저 구하는 것은 불가능하다는 의미입니다.
따라서
- (s’,) -> (s’+ , ) = (s,) // E.g. ( s/2 , * ) -> (s/2,s/2) -> (s, s/2)
- (s+1, ) -> (s,)
에서의 2번 경우는 고려하지 않아도 됩니다.
이러한 이유로 1번의 경우만 고려하면 되기 때문에 코드에서 curr.first + curr.second <= S를 사용합니다.
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
int S;
int check[1002][1002]; //[해당 step에서 화면에 있는 이모티콘 수][클립보드에 있는 이모티콘 수]
int bfs(int start) {
queue<pair<int, int>> q;
check[start][0] = 1;
q.push(make_pair(start, 0));
while (!q.empty()) {
pair<int, int> curr = q.front(); q.pop();
//클릭보드 갱신
if (check[curr.first][curr.first] == 0 && curr.first != curr.second) {
check[curr.first][curr.first] = check[curr.first][curr.second] + 1;
if (curr.first == S) return curr.second;
q.push(make_pair(curr.first, curr.first));
}
//붙혀넣기
if (curr.first + curr.second <= S && check[curr.first + curr.second][curr.second] == 0 ) {
check[curr.first + curr.second][curr.second] = check[curr.first][curr.second] + 1;
if (curr.first + curr.second == S) return curr.second;
q.push(make_pair(curr.first + curr.second, curr.second));
}
//하나 빼기
if (check[curr.first - 1][curr.second] == 0 && curr.first - 1 >= 0) {
check[curr.first - 1][curr.second] = check[curr.first][curr.second] + 1;
if (curr.first - 1 == S) return curr.second;
q.push(make_pair(curr.first - 1, curr.second));
}
}
return -1;
}
int main(void) {
scanf("%d", &S);
int clip = 0;
clip = bfs(1);
printf("%d\n", check[S][clip] - 1);
return 0;
}
