[9465] 스티커

내 풀이

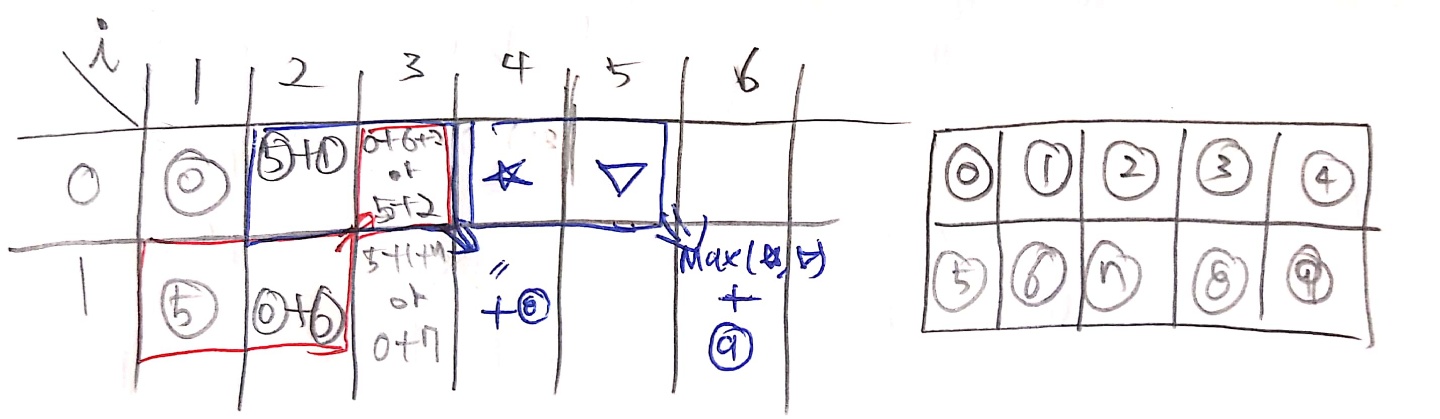
dp[i][j]는 j번 열에서 i 위치의 스티커를 떼어 얻을 수 있는 최대 점수의 합

dp[0][1] = v[0][1];
dp[1][1] = v[1][1];
dp[0][2] = v[1][1] + v[0][2];
dp[1][2] = v[0][1] + v[1][2];

dp[0][3] : 3번째 열에서 0행에 있는 스티커를 얻을 때, dp[1][1]와 dp[1][2] 중 큰 값에 [0][3]번째 스티커의 가치를 추가해야 한다. 3번째 열에서 0행에 있는 스티커를 얻을 때 바로 이전의 스티커가 올 수 있는 위치가 두 군데 뿐이기 때문이다. 위 그림에서 빨간색으로 표시된 (5)과 (0+6) 중 큰 값에 [0][3] 스티커의 가치를 추가해야한다. (0)를 고려하지 않는 것은 (0+6)를 구할 때 이미 (0)을 포함하는 최적의 경우를 고려했기 때문이다.

내 코드

#include <cstdio>
#include <algorithm>
#define MAX(a,b) ((a) > (b) ? (a) : (b))
long long v[2][100001];
long long dp[2][100001];
int t, n;

int main(void) {
	scanf("%d", &t);
	while (t--) {
		scanf("%d", &n);
		for (int i = 0; i < 2; i++) {
			for (int j = 1; j <= n; j++) {
				scanf("%d", &v[i][j]);
			}
		}
		dp[0][1] = v[0][1];
		dp[1][1] = v[1][1];
		dp[0][2] = v[1][1] + v[0][2];
		dp[1][2] = v[0][1] + v[1][2];
		for (int i = 3; i <= n; i++) {
			dp[0][i] = std::max(dp[1][i - 2], dp[1][i - 1]) + v[0][i];
			dp[1][i] = std::max(dp[0][i - 2], dp[0][i - 1]) + v[1][i];
		}
		printf("%d\n", MAX(dp[0][n], dp[1][n]));
	}
	return 0;
}

백준님 풀이

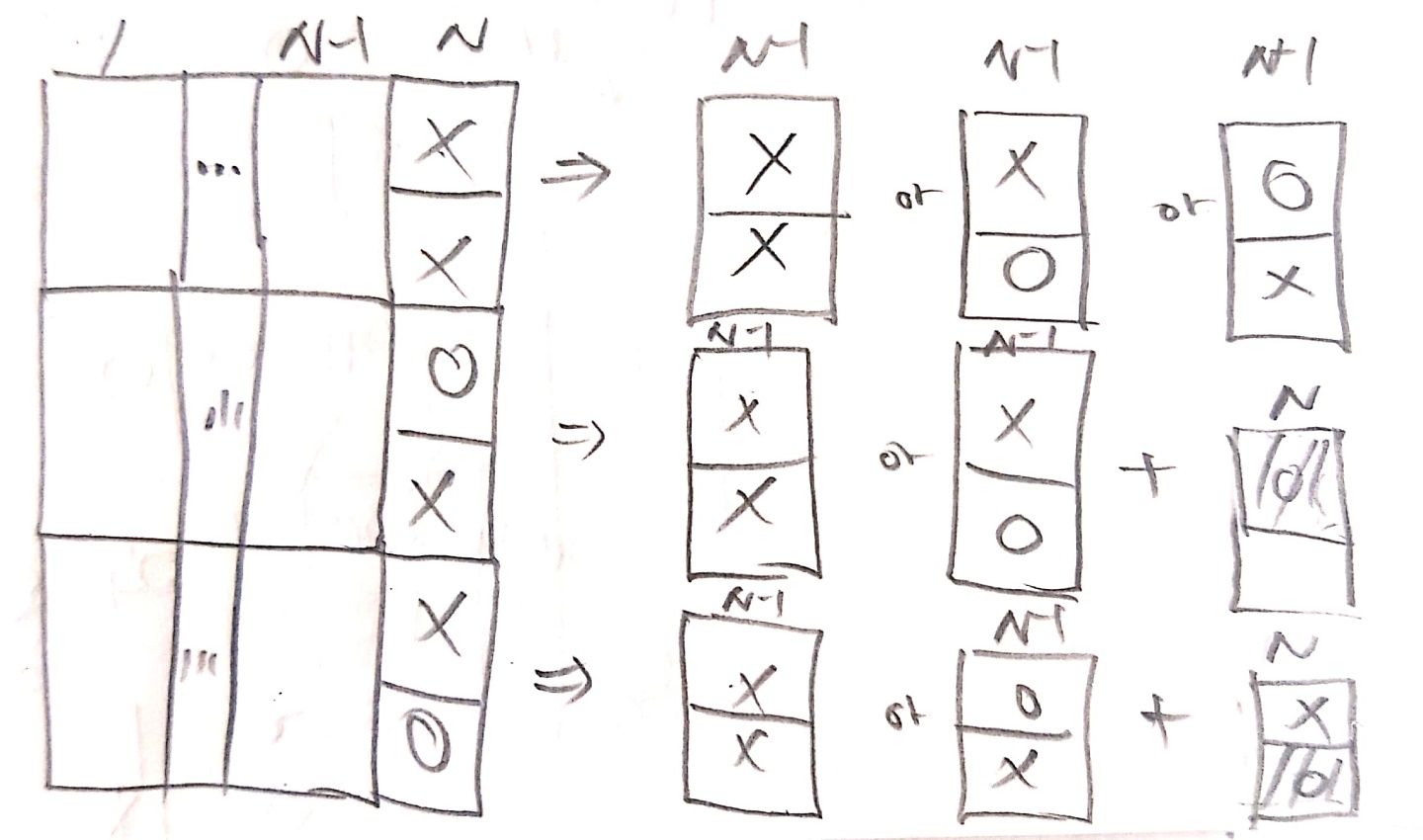
보다 직관적으로 모든 경우를 커버한다. N번째열에서 XX, oX, XO 상태일 때 N-1번째에서 XX,XO,OX 상태 중 가능한 경우를 모두 고려해서 MAX를 구한다.

dp[i][j]는 i상태인 j행에서 얻을 수 있는 가장 큰 가치의 합을 나타낸다.

1. 상태 0 : XX
2. 상태 1 : XO
3. 상태 2 : OX

백준님 코드

#include <cstdio>
#include <algorithm>
using namespace std;
#define MAX(a,b) ((a) > (b) ? (a) : (b))
long long v[2][100001];
long long dp[3][100001];
int t, n;


/*

1. 상태 0 : XX
2. 상태 1 : XO
3. 상태 2 : OX

*/

int main(void) {
	scanf("%d", &t);
	while (t--) {
		scanf("%d", &n);
		for (int i = 0; i < 2; i++) {
			for (int j = 1; j <= n; j++) {
				scanf("%d", &v[i][j]);
			}
		}
		dp[0][1] = 0;
		dp[1][1] = v[1][1];
		dp[2][1] = v[0][1];
		long long a, b, c = 0;
		for (int i = 2; i <= n; i++) {
			a = dp[0][i - 1];
			b = dp[1][i - 1];
			c = dp[2][i - 1];
			dp[0][i] = max(a, max(b, c));
			a = dp[0][i - 1];
			b = dp[2][i - 1];
			c = v[1][i];
			dp[1][i] = max(a,b) + c;
			a = dp[0][i - 1];
			b = dp[1][i - 1];
			c = v[0][i];
			dp[2][i] = max(a, b) + c;
		}
		a = dp[0][n];
		b = dp[1][n];
		c = dp[2][n];
		printf("%d\n", max(a, max(b, c)));
	}
	return 0;
}