[Tree] 트리
개념
싸이클이 없는 그래프를 의미합니다. 따라서 정점이 N개 일 때, 간선의 갯수는 반드시 N-1개입니다.
특성
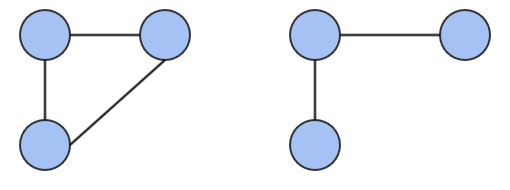
반대로 정점이 N개 간선이 N-1개인 그래프는 트리일까요? 아래 그림은 정점이 6개, 간선이 5개인 그래프이지만 싸이클이 존재합니다. 따라서 연견그래프라는 조건까지 추가적으로 제공되어야 트리라는 것을 보장할 수 있습니다.
- 트리 -> 정점 N개, 간선 N-1개 (O)
- 정점 N개, 간선 N-1개 -> 트리 (X)
- 정점 N개, 간선 N-1개, 연결그래프 -> 트리 (O)
저장 및 탐색
인접리스트를 사용해서 저장합니다. 트리도 그래프이기 때문에 DFS나 BFS 알고리즘을 통해서 탐색을 진행 수 있습니다.
Depth , Height , Leaf
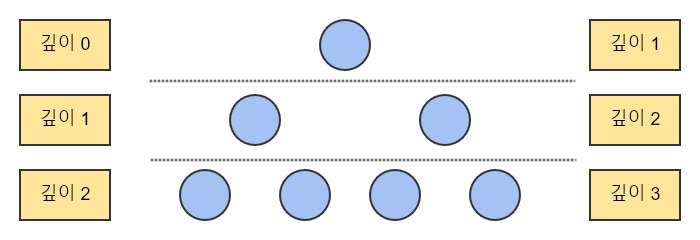
깊이는 위 그림처럼 얼마나 루트로부터 떨어져있는가?를 나타냅니다. 문제의 특성에 따라서 0부터 시자할 수도 1부터 시작할 수도 있습니다.
트리의 높이는 깊이 중에서 가장 깊은 것을 말합니다. 위 그림은 가장 깊은 깊이가 2이므로 높이가 2인 트리라고 할 수 있습니다.
아래는 트리의 깊이를 구하는 코드입니다. BFS와 DFS 둘 다 사용해서 깊이를 구할 수 있습니다.
Leaf 노드인지 판단하는 코드는 bool 탕비 isLeaf를 하나 만들어서 판단합니다.
//BFS 버전
#include <cstdio>
#include <queue>
#include <vector>
using namespace std;
int n;
bool check[500001];
vector<int> v[500001];
queue<int> q;
int a, b;
int depth[500001];
void bfs(int s) {
q.push(s);
while (!q.empty()) {
bool isLeaf = true;
int x = q.front(); q.pop();
printf("방문 %d\n", x);
for (int i = 0; i < v[x].size(); i++) {
int y = v[x][i];
if (check[y] == false) {
isLeaf = false;
check[y] = true;
depth[y] = depth[x] + 1;
q.push(y);
}
}
if (isLeaf) {
printf("%d는 leaf!\n", x);
}
}
}
int main(void) {
scanf("%d", &n);
for (int i = 0; i < n - 1; i++) {
scanf("%d %d", &a, &b);
v[a].push_back(b);
v[b].push_back(a);
}
check[1] = true;
depth[1] = 0;
bfs(1);
for (int i = 1; i <= n; i++) {
printf("%d'th depth : %d\n",i, depth[i]);
}
return 0;
}
//DFS 버전
#include <cstdio>
#include <queue>
#include <vector>
using namespace std;
int n;
bool check[500001];
vector<int> v[500001];
queue<int> q;
int a, b;
int depth[500001];
void dfs(int s) {
bool isLeaf = true;
if (check[s] == true) return;
else {
check[s] = true;
}
printf("%d\n", s);
for (int i = 0; i < v[s].size(); i++) {
int y = v[s][i];
if (check[y] == false) {
isLeaf = false;
depth[y] = depth[s] + 1;
dfs(y);
}
}
if (isLeaf) {
printf("%d 는 leaf!\n", s);
}
}
int main(void) {
scanf("%d", &n);
for (int i = 0; i < n - 1; i++) {
scanf("%d %d", &a, &b);
v[a].push_back(b);
v[b].push_back(a);
}
depth[1] = 0;
dfs(1);
for (int i = 1; i <= n; i++) {
printf("%d'th depth : %d\n",i, depth[i]);
}
return 0;
}
순회
트리 자료구조에만 존재하는 순회라는 개념이 있습니다. 전위순회(Preorder), 중위순회(Inorder), 후위순회(Postorder)라고 합니다.
- 프리오더
- 노드 방문
- 왼쪽 자식 노드를 루트로하는 서브 트리를 프리오더로 방문
- 오른쪽 자식 노드를 루트로하는 서브 트리를 프리오더로 방문
- 인오더
- 왼쪽 자식 노드를 루트로하는 서브 트리를 인오더로 방문
- 노드 방문
- 오른쪽 자식 노드를 루트로하는 서브 트리를 인오더로 방문
- 포스트오더
- 왼쪽 자식 노드를 루트로하는 서브 트리를 포스트오더로 방문
- 오른쪽 자식 노드를 루트로하는 서브 트리를 포스트오더로 방문
- 노드 방문
//TODO
//코드는 나중에 순회를 사용해야하는 문제를 만나면 그때 추가적으로 작성하겠습니다. 간단히 검색으로도 충분히 구할 수 있을 것입니다.
지름
트리에 존재하는 모든 경로 중 가장 긴 것의 길이를 트리의 지름이라고 합니다. 트리의 지름은 탐색 2번으로 구할 수 있습니다. 루트에서 모든 정점까지의 거리를 구합니다. 이때 가장 먼 거리였던 정점을 A라고 합니다. A를 루트로 생각할 때, 모든 정점까지의 거리를 구합니다. 이때 구한 가장 먼 거리가 지름이 됩니다.
- 루트노드 A에서 DFS/BFS를 사용해서 가장 먼 점 B를 구한다.
- B를 루트노드로 생각하고 DFS/BFS를 사용해서 가장 먼점 C를 구한다.
- B에서 C까지의 경로가 지름이다.
증명은 이인복 교수님의 강의 내용을 재구성해서 정리해보겠습니다.
//(TODO)
