[위상정렬] Topological Sort
개념
사이클이 없는 유향 그래프에서, 방향성을 거스르지 않고 정점들을 나열하는 방법입니다. 즉, 방향 그래프에 존재하는 각 정점들의 선행 순서를 위배하지 않으면서 모든 정점을 나열하는 것이다.
DFS를 이용한 구현
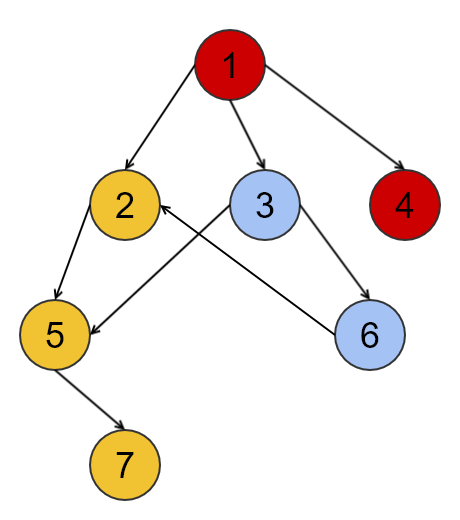
위와 같이 7개의 노드로 구성된 그래프에서 위상정렬을 구해보겠습니다.
- Root인 1번부터 시작해서 BFS를 진행합니다. BFS는 노란색->하늘색->빨간색 순서로 진행된다고 가정합니다.
- 노란색 DFS를 진행합니다. 순서대로 1,2,5,7이 선택되는데 Root노드에서는 아직 모든 DFS는 완료한 것이 아니므로 2,5,7만
역순으로 Stack에 넣어줍니다. - 현재 스택 (top)(2 - 5 - 7)(bottom)
- 하늘색 DFS를 진행합니다. 순서대로 1,3,6이 선택되는데 Root노드에서는 아직 모든 DFS는 완료한 것이 아니므로 3,6만
역순으로 Stack에 넣어줍니다. - 현재 스택 (top)(3- 6 - 2 - 5 - 7)(bottom)
- 빨간색 DFS를 진행합니다. 순서대로 1,4가 선택되는데 Root노드에서는 모든 DFS는 완료했으므로 1,4 모두
역순으로 Stack에 넣어줍니다. - 현재 스택 (top)(1 - 4 - 3- 6 - 2 - 5 - 7)(bottom)
- 이제 stack에서 top에서 하나씩 pop 하면서 접근을 하면 모든 노드를 그래프의 방향성을 위배하지 않고 방문할 수 있습니다.
//인접행렬을 사용한 DFS 코드
//c1 : 인접행렬에서는 a[0][0]의 값이 의미를 가지지 않는다. 그리고 현재 방문한 노드에 대해서 for문을 사용해서 모든 노드의 조건을 확인한다.
void dfs(int x){
check[x] = true;
printf("%d ", x);
for(int i=1; i<=n; i++){
if(a[x][i] == 1 && check[i] == false){
dfs(i);
}
}
}
// 아래는 인접 리스트를 이용한 DFS 코드
void dfs(int x){
check[x] = true;
printf("%d ", x);
for(int i=0; i<a[x].size(); i++){
int y = a[x][i];
if(check[y]==false){
dfs(y);
}
}
}
특징
- DFS로 구현했을 때를 생각하면 하나의 방향 그래프에는 여러 위상 정렬이 가능합니다. 왜냐하면 하늘색 DFS를 먼저 진행할 수도 있기 때문입니다.
- 위상 정렬의 과정에서 선택되는 정점의 순서를 위상 순서(Topological Order)라 합니다.
위상 정렬의 과정에서 그래프에 남아 있는 정점 중에 진입 차수가 0인 정점이 없다면, 위상 정렬 알고리즘은 중단되고 이러한 그래프로 표현된 문제는 실행이 불가능한 문제가 됩니다. -
- 사이클이 있는 그래프는 위상정렬을 할 수 없습니다.
3개의 노드가 사이클을 가지고 있을 때는 위상 순서를 가질 수 없습니다. 쉽게 생각해서 가위-바위-보에서 위상이 있다면 가위-바위-보 문제를 항상 이길 수 있어야 합니다.
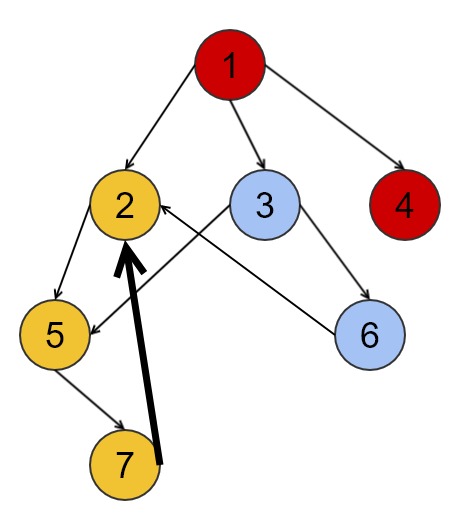
위 그림과 같이 사이클이 있는 경우, 시작점이 존재해야하는 위상정렬의 특성상 시작점이 명확하지 않으므로 위상정렬을 구할 수 없습니다.
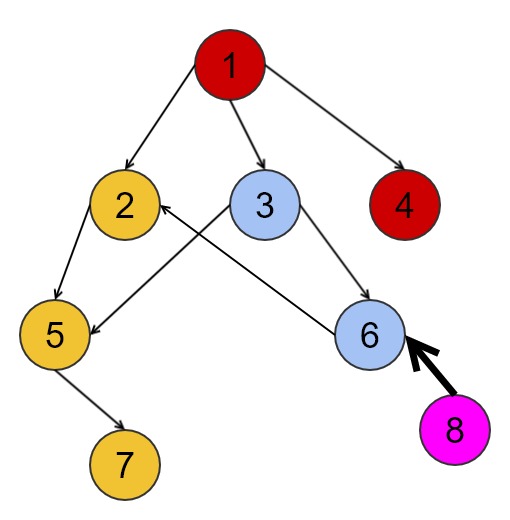
위와 같은 경우는 1번에서 DFS를 진행하고 이후에 8번에서 DFS를 진행하면서 8번 노드의 위상 순서를 결정하면 됩니다.
루트노드를 제외하는 방식으로 구현하는 위상정렬
- 진입차수(indegree)가 0인 노드를 루트노드라고 정의합니다.
- 각 노드의 진입차수를 구해놓는다.
- 루트노드를 먼저 큐에 넣습니다.
- 큐에서 노드를 꺼내 연결된 간선을 모두 지웁니다.
- 간선제거 후 진입차수가 0이 된 정점을 다시 큐에 넣습니다.
- 3.~4. 과정을 반복합니다.
- 큐가 비면 끝납니다.
- 만약 모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재하는 경우입니다.
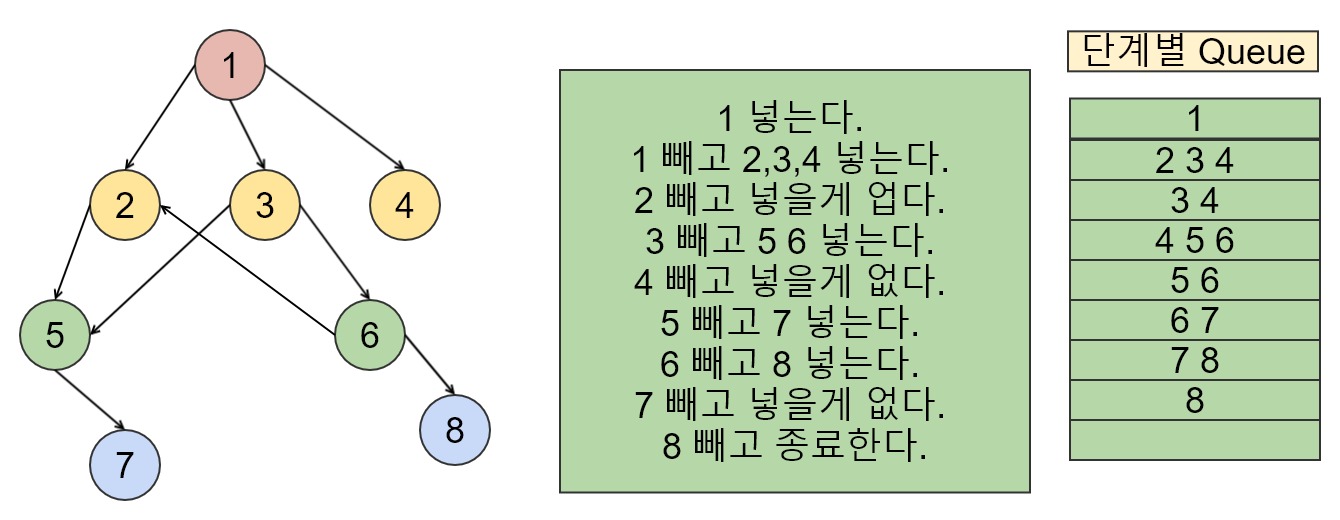
결과적으로는 1 2 3 4 5 6 7 8의 순서대로 모든 노드를 방문하게됩니다. 이렇게 진행하는 것이 1번 실행하고 전체 노드에서 진입차수가 0인 노드들(2,3,4)를 찾은 뒤 이들(2,3,4)을 한 번에 큐에 넣는 등 지저분한 방식을 최적화한 알고리즘입니다.
