[아이디어] Three Archer Problem + 1000 coins
문제 1 : Three Archer
세 명의 궁수 A,B,C가 있습니다. 이들의 명중률은 각각 30%, 60%, 100%입니다. 이들은 서로를 죽이지 못하면 본인들이 죽습니다. A->B->C 순서대로 화살을 쏜다고할 때, A는 어디를 쏴야할까요?
정답 및 풀이
허공.
Case 1. B를 쏜다.
- A가 B를 쏴서 B가 죽는다. : C의 선빵에 의해 A가 죽는다.
- A가 B를 쏴서 B가 안죽는다. : B는 더 위협적인 C를 먼저 쏜다.
- C가 죽는다. : A와 B의 1대1 대결. A가 선빵.
- C가 안죽는다. : C는 B를 죽인다. A와 C의 1대1 대결. A가 선빵
Case 2. C를 쏜다.
- A가 C를 쏴서 C가 죽는다. A와 B의 1대1 대결. B가 선빵
- A가 C를 쏴서 C가 안죽는다. C는 B를 죽인다. A와 C의 1대1 대결. A가 선빵
위의 모든 경우 중 A가 살 가장 높은 가능성은 B와 1대1 대결을 하면서 선빵을 날리는 경우입니다. 따라서 B가 죽지 않고 C를 죽여주는 상황을 기대해야합니다. 따라서 A는 첫 발에서 아무도 안죽이는 것이 이득입니다.
문제 2 : 1000 coins
5명의 사람 A,B,C,D,E가 있다. A부터 E까지의 순서대로 동전을 어떻게 나눠가질지 결정을 해서 모두에게 제안을 합니다. 이때 과반수의 이상을 얻지 못한다면 그 사람은 아무것도 얻지 못하고 분배의 대상에서 제외됩니다. 아래 설명에서는 죽음이라고 표현했습니다. 각자의 상황에서 이들은 어떤 분배 방식을 제안할까요?
정답 및 풀이
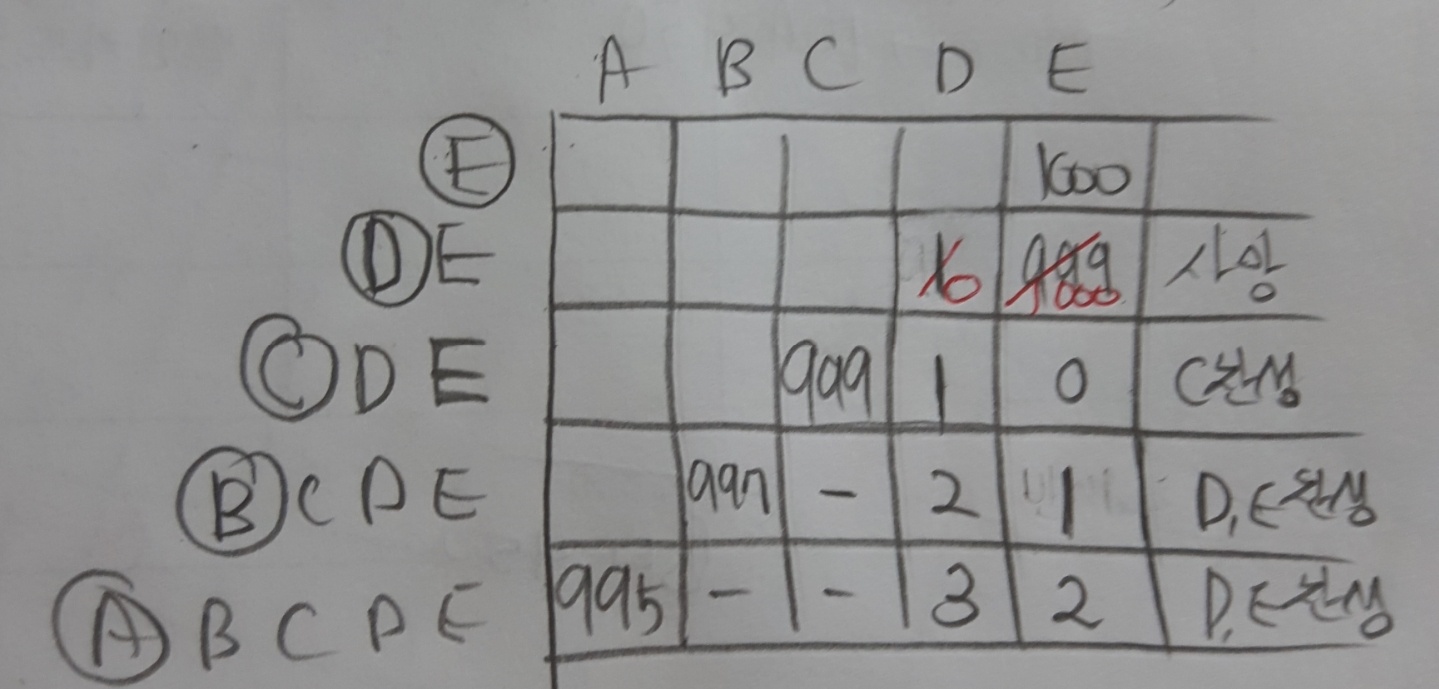
거꾸로 생각해보겠습니다. 위 표의 각 row에는 어떤 사람이 제안을 하는지 원이 쳐져있고, 어떤 사람들이 남아있는지 표현되어 있습니다. 각 col의 위에는 row에서 원이 쳐진 사람이 누구에게 얼마를 주는 제안을 하는지가 표현되어 있습니다.
- E가 혼자 있습니다. E는 모두 자기가 가지고 싶어서 (0,0,0,0,1000)을 제안합니다.
- D,E가 있습니다. D가 어떤 제안을 하던지 E는 거부를 하면됩니다. 그러면 D는 죽고 1.과 같이 혼자 가져갈 수 있습니다.
- C,D,E가 있습니다. C는 D가 자신(C)의 제안을 거절하면 본인(D)이 죽는 것을 알고 있습니다. 그래서 죽는 것보다는 나은 1개만을 줍니다. D는 아쉽지만 이를 받아들여야 이득입니다. (999,1,0)
- B,C,D,E가 있습니다. C는 B를 죽이고 싶습니다. B의 제안을 거절하면 자기(C)가 999개를 가질 수 있는 방법을 알고있으니까요. B도 이를 알고 있습니다. 그래서 B는 C를 제외한 D와 E에게 제안을 합니다. 내가 죽어서 C의 제안을 받아들이는 것보다는 좋은 제안을 합니다. (998,0,2,1)
- A,B,C,D,E가 있습니다. B는 A를 죽이고 싶습니다. A도 이를 알고 있습니다. 자신이 과반수를 얻기 위해서는 두 명의 지지가 필요한데, A가 죽었을 때 C,D,E 세 명이 받을 수 있는 코인의 갯수를 확인합니다. A가 죽으면 C는 아무것도 받지 못합니다. 따라서 C에게 1개만 주면 찬성해줄 것입니다. D와 E도 A가 죽었을 때 받을 수 있는 갯수에서 1개만 더 준다면 A를 반드시 지지해줄 것입니다. 따라서 답은 C,D,E 중 두 명에게 A가 죽었을 때 받을 수 있는 양에서 1개를 더 준다.입니다. 저는 D와 E에게 1개씩을 더 주어서 (995,0,0,3,2)의 제안을 생각해봤습니다.
