[아이디어] Subset Sum

문제

n개의 서로 다른 숫자가 주어져 있다. 이 중 k개를 더했을 때 정확하게 합이 S가 되는 것이 있는지 구하는 프로그램을 작성하시오.

$O(nlogn)$ 풀이 : K = 2인 경우

1. 모든 숫자를 정렬
2. two pointers : 제일 작은 값과 제일 큰 값을 가리킨다. 이들을 a, b라고 하자.

• a+b < S : a를 더 큰 숫자로 바꾼다.
• a+b > S : b를 더 작은 숫자로 바꾼다.
• a+b ==S : 정답
• a<=b를 만족해야하므로 a와 b가 만나는 순간까지 S합이 S인 경우가 없다면 없다.

예를 들어서 2 3 4 5 인 경우(S=9):
시작 a=2, b=5일 때 합이 9보다 작으므로 a=3으로 올리고 a=4로 올린다.

$O(KNS)$ 풀이 : 숫자를 중복해서 뽑는 경우

숫자들이 {1,2,3,5}와 같이 주어졌다고 가정하겠습니다. 이들 중에서 S=6을 찾아야 합니다.

DP 테이블의 dp[i][j]는 다음과 같은 의미를 가집니다. 숫자 i개를 가지고 합 j를 만들 수 있으면 1, 아니면 0

이 문제의 핵심은 i개로 S를 만들 수 있다면, i개 중 1개의 값이 a일 때 이를 제외한 i-1개로 만들 수 있는 값은 S-a이다. 입니다.

1. dp[i][j]의 정의에 따라서 i의 범위는 [0,K] 이고, j의 범위는 [0,S]입니다.
2. dp[i][j]의 정의에 따라서 dp[1][j]의 값들은 쉽게 알 수 있습니다. 1,2,3,5에 대응하는 칸 모두 1입니다.
3. 다음은 파란색을 보면 됩니다. 1을 제외한 숫자 1개로 2,3,5를 만들 수 있습니다. 여기에 숫자 1을 더하면 3,4,6을 만들 수 있습니다.
4. 다음은 빨간색을 보면 됩니다. 2를 제외한 숫자 1개로 3,5를 만들 수 있습니다. 여기에 숫자 2를 더하면 5,7이 되는데 7은 범위를 벗어나므로 무시합니다.
5. 3과 5도 같은 방법으로 진행합니다. 범위에 벗어나므로 의미는 없습니다.
6. 3.~5.의 과정은 문제에서 주어진 N개의 값에 대해서 DP[i]줄을 구하기 위해서 DP[i-1]번째 줄에 값을 더해보는 과정을 의미합니다. 잘 이해가 안되면 아래를 봅니다.

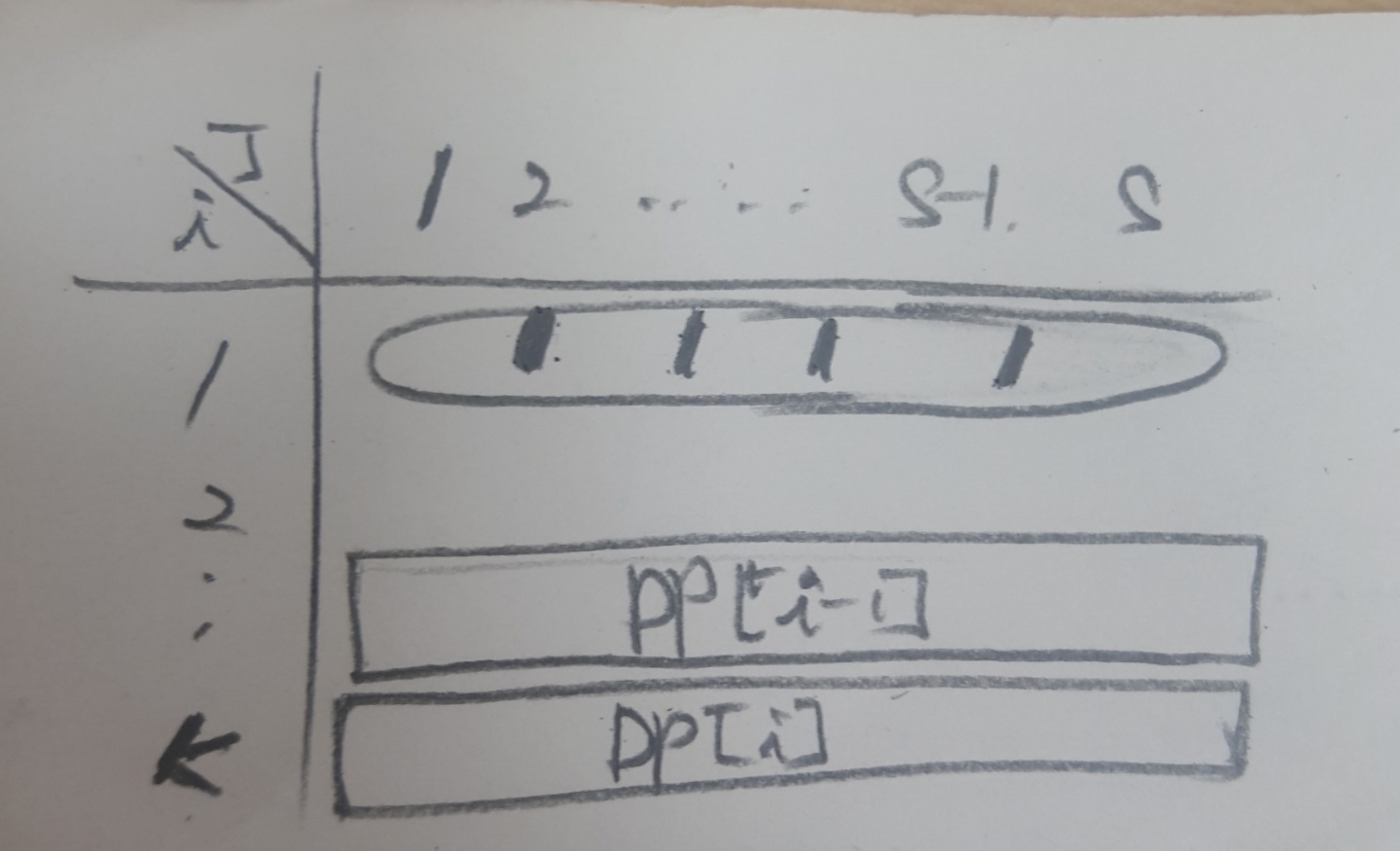
1. dp[i][j]줄을 구하기 위해서 dp[0][j]에서 1을 가진 모든 값들을 dp[i-1][j]의 모든 값에 대응시켜봅니다.
2. 1번의 과정은 dp[0][j]에서 1을 가진 모든 값들은 문제에서 주어진 N과 같고(가장 큰 N <=S일 때), j의 범위를 $[0,S]$로 정의했으므로 $O(NS)$를 가집니다.
3. dp[i][[j]만 구하는 것이 아니라 dp[0][j]부터 dp[k][j]까지 k+1줄을 구해야 하므로 최종적인 시간 복잡도는 $O(NSK)$가 됩니다.

최종적으로 dp의 점화식을 정리하면 다음과 같습니다.

if(dp[i-1][j-a] == 1 && dp[1][a] == 1){
  dp[i][j] == 1
}