[LCS] 최장 공통 부분 서열

정의

• 부분 서열 (subsequence) : 주어진 서열에서 0개, 또는 그 이상의 글자를 지워서 얻을 수 있는 서열

• 공통 부분 서열 (common subsequence) : 두 서열이 주어졌을 때, 두 서열에 공통인 부분 서열

• 최장 공통 부분 서열 (LCS) : 공통 부분 서열 중 가장 길이가 긴 것

알고리즘

완전 탐색

길이가 $N$인 서열은 $2^{N}$개의 부분 서열이 존재한다. 각 문자가 들어가고 안들어갈 수 있는 경우 두 가지가 있기 때문이다.

DP

만약 두 문자열의 길이가 1이라면, 두 문자가 같을 때 LCS의 길이는 1이고 두 문자가 다를 때 0이다.

두 문자열의 길이가 1 이상일 때는 마지막에 덧붙히는 문자에 따라서 LCS의 결과가 달라진다. A 문자열에서 i 번째까지 B 문자열에서 j까지 비교해서 현재까지 얻은 LCS에서 각각 i+1와 j+1번째의 문자를 붙힐 때, 이 두 문자가 같으면 LCS가 +1되고 아니라면 그대로 남는다.

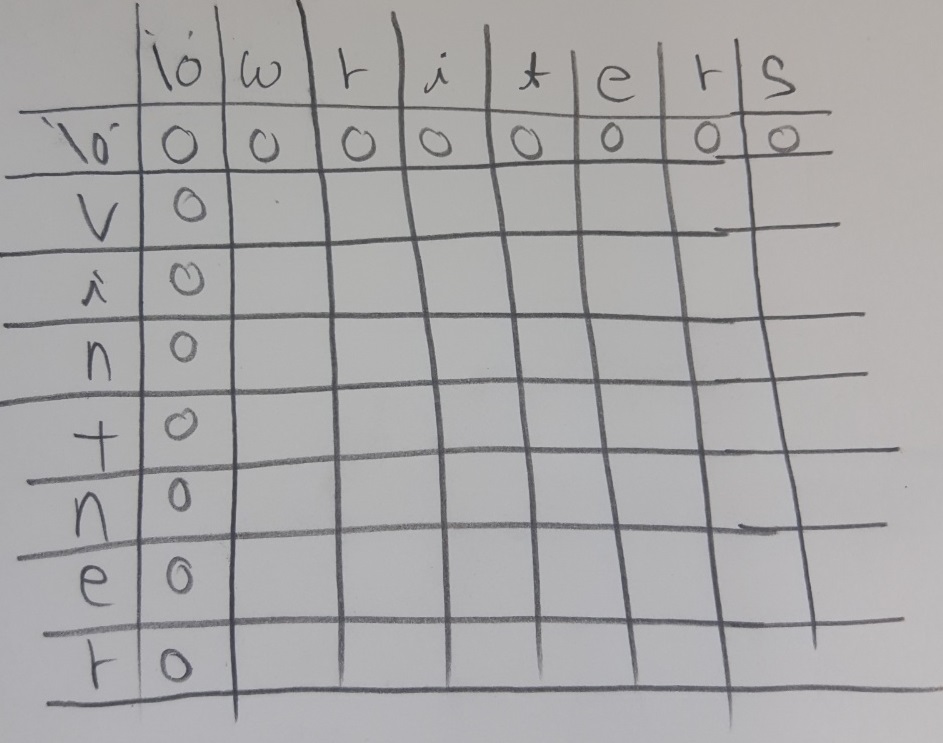
위 그림은 DP 테이블입니다. 각 칸은 A문자열에서 0~i번째까지 문자열과 B문자열에서 0~j까지 문자열의 LCS의 길이를 의미합니다. 지금 0으로 적힌 부분은 모두 ‘\0’ 널문자와의 LCS의 길이가 0이기 때문에 0으로 표기했습니다. ‘\0’을 넣은 것은 DP 테이블 전체에 대해서 아래에서 설명할 알고리즘을 일관되게 적용하기 위함입니다.

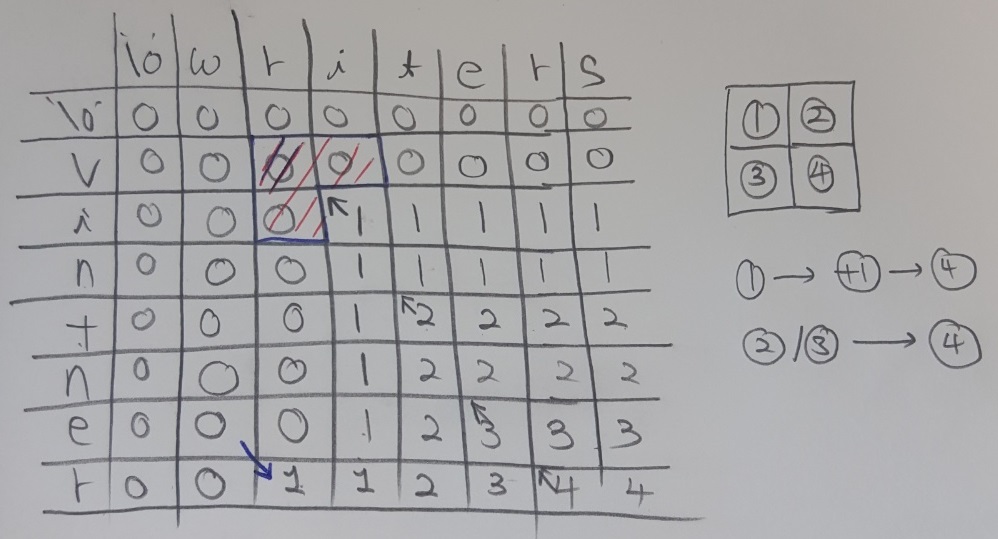
위 그림은 DP 테이블을 채운 형태입니다. 채우는 알고리즘은 오른쪽에 그려져있는 1,2,3,4를 보면 나와있습니다.

1. 두 문자열에 대해서 마지막에 추가한 문자가 같으면 dp[i][j] = dp[i-1][j-1] + 1;
2. 아니라면, 두 문자열에 대해서 마지막에 추가한 문자가 다른 경우
3. dp[i][j+1] : str1의 [0,i]까지와 str2의 [0,i+1]까지 비교된 결과
4. dp[i+1][j] : str1의 [0,i+1]까지와 str2의 [0,i]까지 비교된 결과
5. 이 둘 중 큰 값을 dp[i+1][j+1]에 저장
6. 0이 아닌 모든 숫자를 적는 경우에 대해서 1,2,3 중 어느 방향의 값을 보고 4번의 값을 적었는지 화살표로 표시해둡니다. 이 화살표는 LCS의 길이를 구한 후 LCS가 어떤 문자들로 구성되는지 확인할 때 사용합니다.

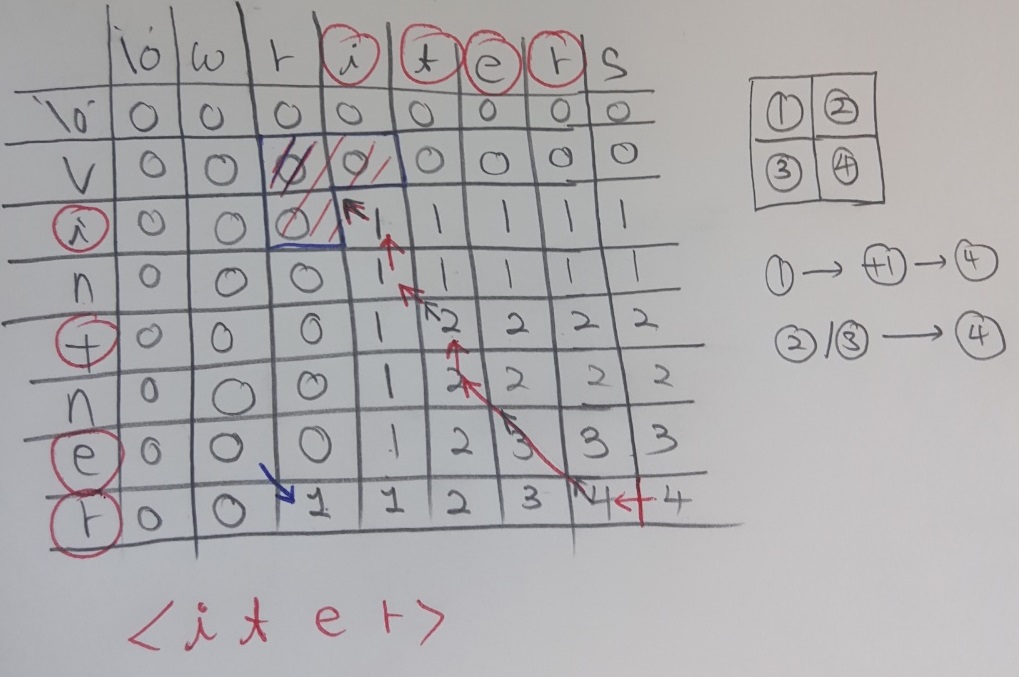
이 사진은 4.번에서 그려분 화살표를 보고 LCS를 구성하는 문자가 “iter”임을 찾은 모습입니다. 화살표를 따라가면서 1.~2.번 알고리즘에 의해서 숫자가 커진 곳을 찾습니다. 해당 칸의 row와 col을 보면 이번 비교에서 추가된 문자가 같음을 확인할 수 있습니다. 이러한 방식으로 LCS를 구성하는 문자들을 뒤에서부터 찾을 수 있습니다.

시간복잡도

D[i][j]를 구하기 위해서는 세 값 D[i-1][j], D[i][j-1],D[i-1][j-1]을 구해야 하고, 셋 중에 제일 큰 값을 구해야 하므로 O(1) 시간. 이 비교를 두 문자열의 길이의 곱만큼 진행하므로 $O(|T1||T2|)$시간.

코드 : DP

//두 문자열과 두 문자열의 길이를 Param으로 전달
int lcs( char *X, char *Y, int m, int n )
{
  int L[m+1][n+1]; //L은 LCS를 의미함
  int i, j;
  for (i=0; i<=m; i++) {
    for (j=0; j<=n; j++) {
      if (i == 0 || j == 0)
        L[i][j] = 0;
      else if (X[i-1] == Y[j-1])
        L[i][j] = L[i-1][j-1] + 1;
      else
        L[i][j] = max(L[i-1][j], L[i][j-1]);
    }
  }
  return L[m][n];
}

코드 : Recursive

Recursive로 푸는 경우 이미 구한 칸의 답을 다시 구하는 경우가 존재하므로 DP로 푸는 것이 최적입니다.

#include <string>
int lcs( char *X, char *Y, int m, int n )
{
  if (m == 0 || n == 0)
   return 0;
  if (X[m-1] == Y[n-1])
    return 1 + lcs(X, Y, m-1, n-1);
  else
    return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n));
}

int main()
{
  char X[] = "AGGTAB";
  char Y[] = "GXTXAYB";
  int m = strlen(X);
  int n = strlen(Y);
  printf("Length of LCS is %d\n", lcs( X, Y, m, n ) );
  return 0;
}

비슷한 문제 : 금화 모으기

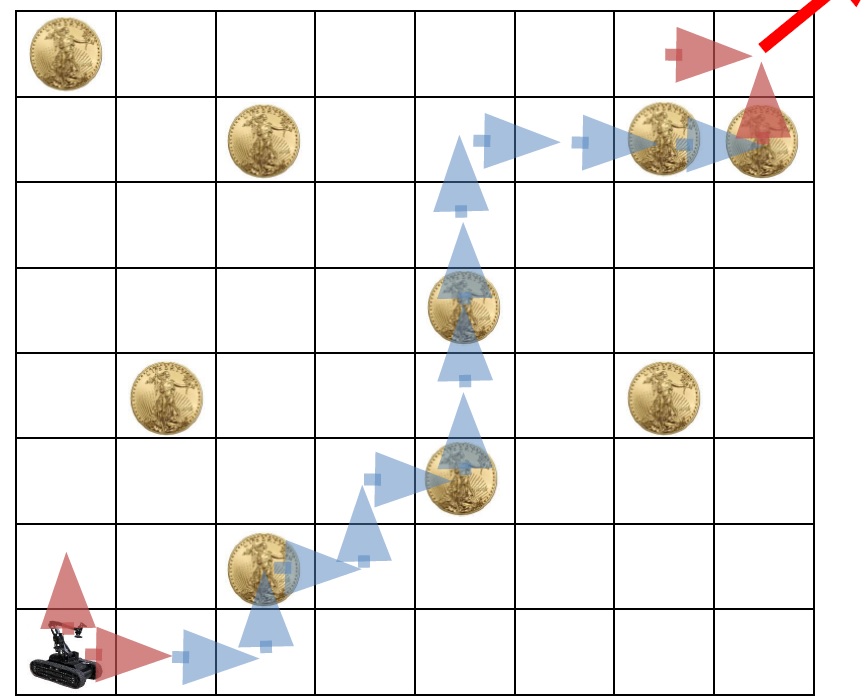
위 알고리즘이 3칸의 값을 확인했다면, 금화 모으기 문제는 왼쪽과 아래의 두 칸의 정보만 확인합니다. 그리고 현재의 칸에 금화가 있다면 두 값의 최대값+1 없다면 그냥 두 값의 최대값을 적습니다.

• if (i, j)에 금화 : D[i][j] = max(D[i-1][j], D[i][j-1]) + 1
• if (i, j)에 금화 : D[i][j] = max(D[i-1][j], D[i][j-1]) + 0

금화 모으기 코드

#include <iostream>
#include <vector>
using namespace std;
int main()
{
  vector<pair<int,int>> coins;
  coins.push_back(make_pair(1, 8)); coins.push_back(make_pair(2, 4));
  coins.push_back(make_pair(3, 2)); coins.push_back(make_pair(3, 7));
  coins.push_back(make_pair(5, 3)); coins.push_back(make_pair(5, 5));
  coins.push_back(make_pair(7, 4)); coins.push_back(make_pair(7, 7));
  coins.push_back(make_pair(8, 7));
  int m[9][9]; //
  int D[9][9];

  //배열 초기화
  for (int i = 0; i < 9; i++){
    for (int j = 0; j < 9; j++){
      D[i][j] = m[i][j] = 0;
    }
  }

  //모든 코인의 위치 저장
  for (auto c: coins){
    m[c.first][c.second] = 1;


  //DP 테이블 채우기
  for (int i = 1; i < 9; i++)
    for (int j = 1; j < 9; j++)
     D[i][j] = max(D[i-1][j], D[i][j-1]) + m[i][j];
  
  //최우상단 값 출력
  cout << D[8][8] << endl;
}